中考数学学霸笔记——构造全等三角形的五种常用方法

方法一：倍长中线法

例1：如图，△ABC中，D为BC的中点．

（1）求证：AB+AC＞2AD；

（2）若AB＝5，AC＝3，求AD的取值范围．

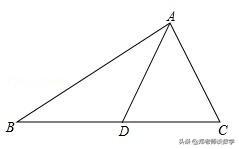
【分析】（1）延长AD至E，使DE＝AD，构造△ADC≌△EDB，再根据三角形的三边关系可得AB+AC＞2AD；

（2）直接利用三角形的三边关系：三角形两边之和大于第三边，三角形的两边差小于第三边可得5﹣3＜2AD＜5+3，再计算即可．

【解答】（1）证明：由BD＝CD，再延长AD至E，使DE＝AD，

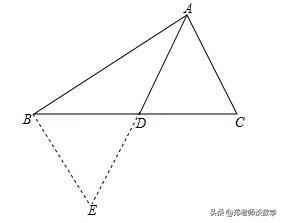
∵D为BC的中点，

∴DB＝CD，

在△ADC和△EDB中，

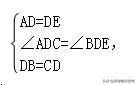
∴BE＝AC，

在△ABE中，∵AB+BE＞AE，

∴AB+AC＞2AD；

（2）∵AB＝5，AC＝3，

∴5﹣3＜2AD＜5+3，

∴1＜AD＜4．

【点评】此题主要全等三角形的判定与性质，关键是正确作出辅助线，延长中线，是一种常见的辅助线．

方法二：翻折法

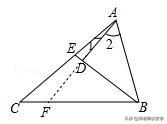
例2：如图．在△ABC中，BE是角平分线，AD⊥BE，垂足为D，求证：∠2＝∠1+∠C．

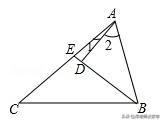
【分析】延长AD交BC于点F（相当于将AB边向下翻折，与BC边重合，A点落在F点处，折痕为BE），由BE是角平分线、AD⊥BE可知△ABF是等腰三角形且∠2＝∠AFB，根据∠AFB＝∠1+∠C可得证．

【解答】证明：如图，延长AD交BC于点F，

∵BE是角平分线，AD⊥BE，

∴△ABF是等腰三角形，且∠2＝∠AFB，

又∵∠AFB＝∠1+∠C，

∴∠2＝∠1+∠C．

【点评】本题主要考查等腰三角形的判定与性质，解题的关键是掌握等腰三角形三线合一的性质．

方法三：旋转法

例3：正方形ABCD中，E为BC上的一点，F为CD上的一点，BE+DF＝EF，求∠EAF的度数．

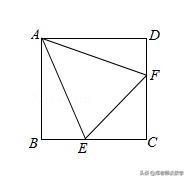
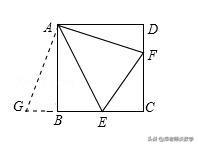
【分析】延长EB使得BG＝DF，易证△ABG≌△ADF（SAS）（相当于将△ADF绕着点A顺时针旋转90°得到△ABG）可得AF＝AG，进而求证△AEG≌△AEF可得∠EAG＝∠EAF，再求出∠EAG+∠EAF＝90°即可解题．

【解答】解：延长EB使得BG＝DF，连接AG，

在△ABG和△ADF中，

由

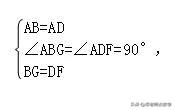
△ABG≌△ADF（SAS），

∴∠DAF＝∠BAG，AF＝AG，

又∵EF＝DF+BE＝EB+BG＝EG，AE＝AE，

在△AEG和△AEF中，

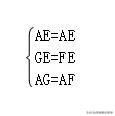
∴△AEG≌△AEF（SSS），

∴∠EAG＝∠EAF，

∵∠DAF+∠EAF+∠BAE＝90°

∴∠EAG+∠EAF＝90°，

∴∠EAF＝45°．

答：∠EAF的角度为45°．

【点评】本题考查了正方形各内角均为直角，考查了全等三角形的判定，考查了全等三角形对应边、对应角相等的性质，本题中求证∠EAG＝∠EAF是解题的关键．

方法四：构造法

例4：如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，∠ABC＝45°，点D为BC的中点，CE⊥AD于点E，其延长线交AB于点F，连接DF．求证：∠ADC＝∠BDF．

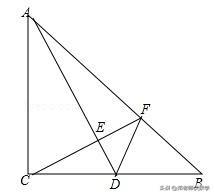
【分析】作BG⊥CB，交CF的延长线于点G，由ASA证明△ACD≌△CBG，得出CD＝BG，∠CDA＝∠CGB，证出BG＝BD，∠FBD＝∠GBF＝∠CBG，再由SAS证明△BFG≌△BFD，得出∠FGB＝∠FDB，即可得出结论．

【解答】证明：作BG⊥CB，交CF的延长线于点G，如图所示：

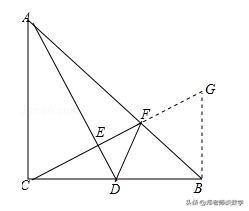
∵∠CBG＝90°，CF⊥AD，

∴∠CAD+∠ADC＝∠BCG+∠ADC＝90°，

∴∠CAD＝∠BCG，

在△ACD和△CBG中，

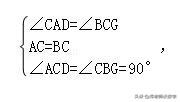
∴△ACD≌△CBG（ASA），

∴CD＝BG，∠CDA＝∠CGB，

∵CD＝BD，

∴BG＝BD，

∵∠ABC＝45°，

∴∠FBD＝∠GBF＝∠CBG，

在△BFG和△BFD中，

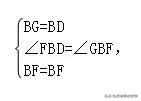
∴△BFG≌△BFD（SAS），

∴∠FGB＝∠FDB，

∴∠ADC＝∠BDF．

【点评】本题考查了全等三角形的判定与性质、等腰直角三角形的性质；本题有一定难度，需要通过作辅助线两次证明三角形全等才能得出结论．

方法五：截长补短法

例5：如图，AB∥CD，CE，BE分别平分∠BCD和∠CBA，点E在AD上，求证：BC＝AB+CD．

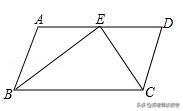
【分析】在BC上取点F，使BF＝BA，连接EF，由角平分线的性质可以得出∠1＝∠2，从而可以得出△ABE≌△FBE，可以得出∠A＝∠5，进而可以得出△CDE≌△CFE，就可以得出CD＝CF，即可得出结论．

【解答】证明：在BC上取点F，使BF＝BA，连接EF，

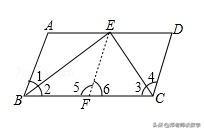
∵BE、CE分别是∠ABC和∠BCD的平分线，

∴∠1＝∠2，∠3＝∠4．

在△ABE和△FBE中，

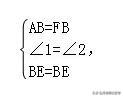
∴△ABE≌△FBE（SAS），

∴∠A＝∠5．

∵AB∥CD，

∴∠A+∠D＝180°，

∴∠5+∠D＝180．

∵∠5+∠6＝180°，

∴∠6＝∠D．

在△CDE和△CFE中，

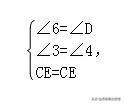
∴△CDE≌△CFE（AAS），

∴CF＝CD．

∵BC＝BF+CF，

∴BC＝AB+CD．

【点评】本题考查了角平分线的性质的运用，全等三角形的判定及性质的运用，解答时运用截取法正确作辅助线是关键．

以上五种方法是比较常用的方法，希望对你的解题有所帮助～～～～