「初中数学」利用含30°角的直角三角形解题的几种技巧

在初中数学中有这样一个定理:在直角三角形中，若一个锐角为30°，则它所对的边是斜边的一半.它通过角的关系揭示出了边的关系，从角的类别跨出到了边的类别，建立了不同类别之间的联系，所以非常重要，那么在证明线段之间的倍分关系时，我们就要注意提醒自己，题中是否含有30°、60°或120°的特殊角，或者通过某种方法构造含30°的直角三角形.这一定理运用比较广泛，下面结合八年级的习题分别说明。

一.直接运用含30°角的直角三角形的性质

1.如图，在等边三角形ABC中，AE=CD，AD，BE相交于点P，BQ⊥AD于点Q.

求证:BP=2PQ.

【分析】由等边三角形ABC知，AB=AC=BC，∠BAC=∠ABC=∠ACB=60°且AE=CD，显然△ACD≌△BAE.结论要证BP=2PQ，想到在直角三角形BQP中，找30°角或60°，而∠BPQ=∠ABP+∠BAP，由△ACD≌△BAE，可知∠ABP=∠CAD，所以∠BPQ=∠BAP+∠CAD=∠BAC=60°则达到目的.

证明:∵△ABC为等边三角形，∴AC=AB，∠C=∠BAC=60°，又AE=CD，∴△ACD≌△BAE，∴∠CAD=∠ABE，∵∠CAD+∠BAP=∠BAC=60°，∴∠ABE+∠BAP=∠BPQ=60°，∵BQ⊥AD，∴∠BQP=90°，∴∠PBQ=90°一∠BPQ=30°，∴BP=2PQ.

2.如图，在△ABC中，AB=AC，∠BAC=90°，BD=AB，∠ABD=30°.

求证:AD=DC.

【分析】欲证，AD=CD，想到什么:等腰三角形三线合一;想到证底角相等？不管你想到哪个定理和性质，还得联系其他条件，条件有，等腰直角三角形BAC，有∠ABD=30°，这些条件又与结论怎样联系呢？那我们就要画辅助线试着分析一下，因为∠ABD=30°，AB=BD，可得，∠BAD=∠BDA=75°，过点A作AE⊥BD于E，E为垂足，使30°的角处于直角三角形中，则有∠EAD=15°，AE=AB/2，又分析出∠CAD=15°，则AD是∠CAE的角平分线，而DE⊥AE，于是想到过点D作DF⊥AC于F，则可证△EAD≌△FAD，得AF=AE=AB/2=AC/2，∴F是AC的中点，∴DF垂直平分AC，∴AD=DC，得证.如图

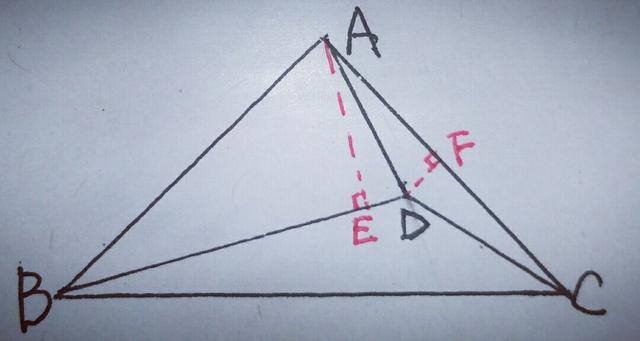
证明:过点A作AE⊥BD于E，过点D作DF⊥AC于F，∴∠AEB=∠AED=∠AFD90°则在Rt△AEB中，∵∠ABD=30°，∴AE=AB/2，又∵AB=AC，则AE=AC/2，在△ABD中，∵AB=BD，∠ABD=30°，∴∠BAD=1/2(180°一30°)=75°，∵∠BAC=90°，∴∠DAC=15°，而在Rt△AED中，可知∠BAE=60°，∴∠EAD=15°，所以根据∠DAC=∠EAD=15°，∠AED=∠AFD=90°，AD=AD，可得△EAD≌△FAD，∴AF=AE=AC/2，即F是AC的中点，∴DF垂直平分AC，∴AD=DC.

那么依据∠DAC=∠DCA是否也可证AD=DC呢？只要同学们善于分析，还是可以的，下面给出一种作辅助线的方法，希望同学们仔细体会.以BC为边在△ABC的同侧作等边三角形BEC，连接AE，如图，

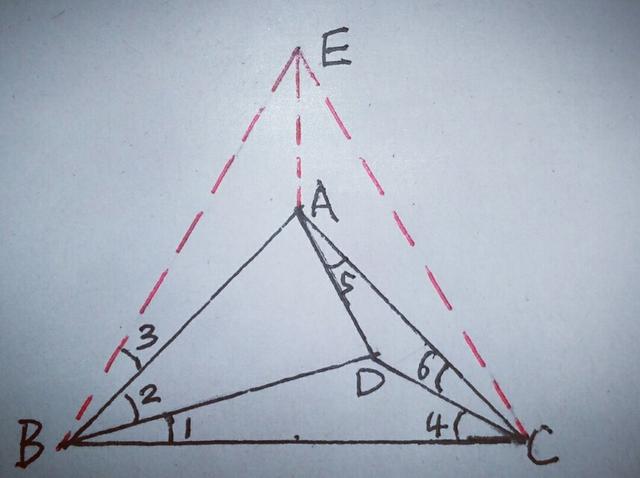
由于正三角形，等腰直角三角形的对称性可知，EA平分∠BEC，所以∠BEA=30°，由于∠ABC=60°，∠ABC=45°，∠ABD=30°，所以∠EBA=∠CBD=15°，而AB=BD，BE=BC，∴△EBA≌△CBD，∴∠BCD=∠BEA=30°，则∠ACD=15°，由上边证得知∠DAC=15°，∴∠DAC=∠DCA，∴AD=DC，此法关键是作出一个等边三角形，有同学要问，你怎么就知道作等边三角形呢？显然我也是学来的，多总结，多归纳，多记忆，多体会，你也会知道这种辅助线。

【对应练习】

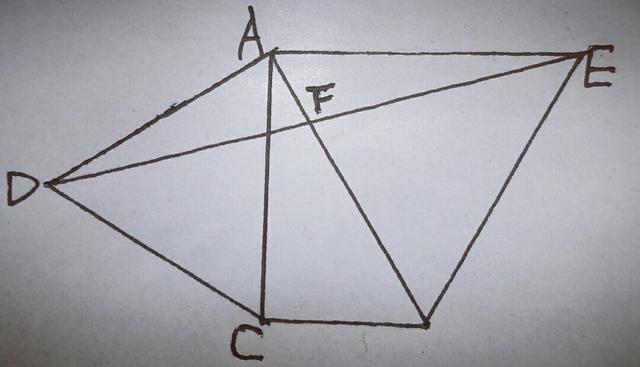
1.如图，在△ABC中，∠ACB=90°，∠CAB=30°，以AC，AB为边在△ABC外侧作等边△ACD和等边△ABE，连接DE交AB于F，求证:DF=EF.

二.连线段构造含30°角的直角三角形

3如图，在△ABC中，AB=AC，∠BAC=120°，D为BC的中点，DE⊥AC于E，AE=8，求CE的长.

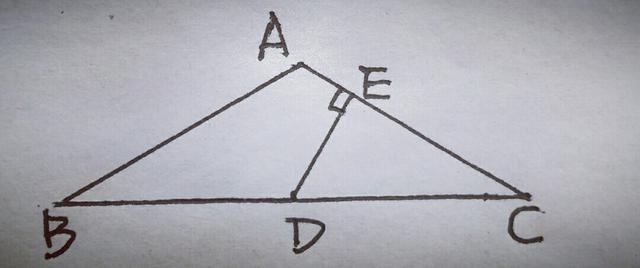
【分析】本题不难，∵AB=AC，D为BC的中点，所以很自然的要连接AD，则AD⊥BC，而∠BAC=120°，∴∠C=30°，∠DAC=60°，∠ADE=30°，因为AE=8，所以AD=16，所以AC=32，则CE=AC一AE=32一8=24.

4.如图，已知在△ABC中，AB=AC，∠A=120°，DE垂直平分AB交AB于点D，交BC于点E，求证:CE=2BE.

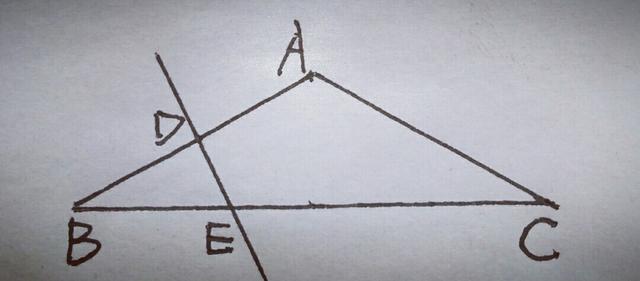
【分析】条件有，DE垂直平分AB，根据"垂直平分线上的点，到线段两个端点的距离相等，所以连接AE，则BE=AE，因为∠A=120°，则∠B=∠C=30°，同时∠BAE=∠B=30°，则∠EAC=90°，所以CE=2AE=2BE.

三.延长两边构造含30°角的直角三角形

5.如图，在四边形ABCD中，AD=4，BC=1，∠A=30°，∠B=90°，∠ADC=120°，求CD的长.

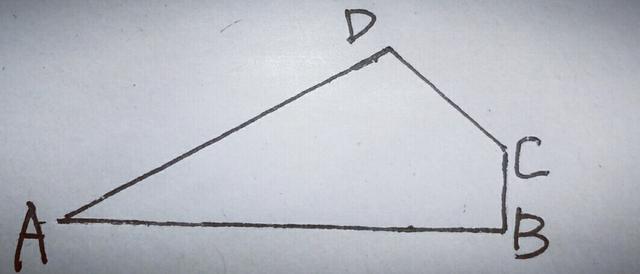
【分析】由于∠A=30°，∠B=90°，依托图形，延长BC，延长AD，交于点E，构造含30°角的直角三角形，如下图

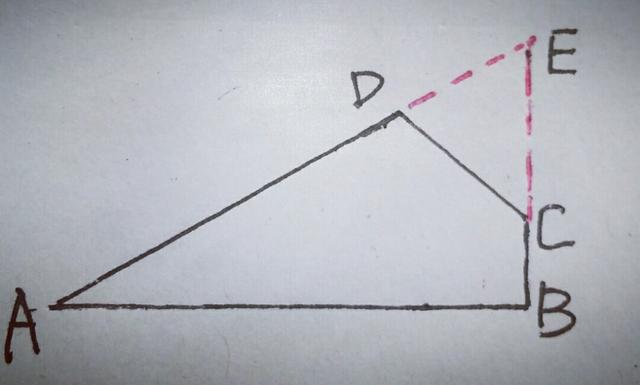
则AE=2BE，∠E=60°，又∵∠ADC=120°，∴∠EDC=60°，∴三角形DEC为等边三角形，∴DC=DE=CE，设DC=a，则4十a=2(1十a)，解得a=2，即DC=2，本题还可作垂线段等构造含30°角的直角三角形，有好多种方法， 同学们自己做一下.

四.作垂线段构造含30°角的直角三角形

6.如图，在四边形ABCD中，∠B=90°，DC∥AB，AC平分∠BAD，∠DAB=30°，求证:AD=2BC.

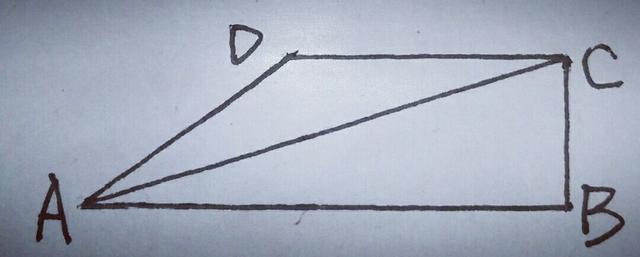
【分析】此题有AC平分∠BAD，CD∥AB，则出等腰△ADC(角分平，等腰呈)，又∠B=90°，想到角平分线上的点到角两边的距离相等，所以过点C作CE⊥AD，交AD延长线于E，则BC=CE，而AD=DC，又DC∥AB，∠DAB=30°，∴DC=2BE，则AD=2BC.(过性质，定理，引出相应的辅助线，成功的实现了转化).

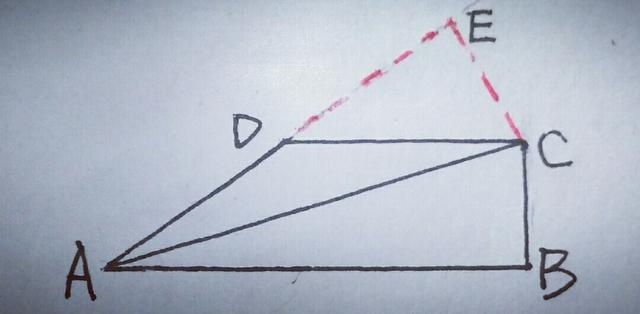
7.如图，在△ABC中，BD=DC，AD⊥AC，∠BAD=30°，求证:AC=AB/2.

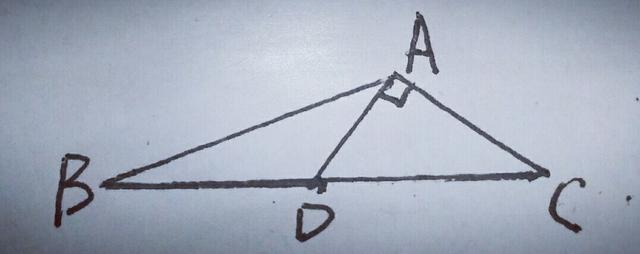
【分析】∵∠BAD=30°，∴过点B作BE⊥AD，交AD的延长线于点E，如图

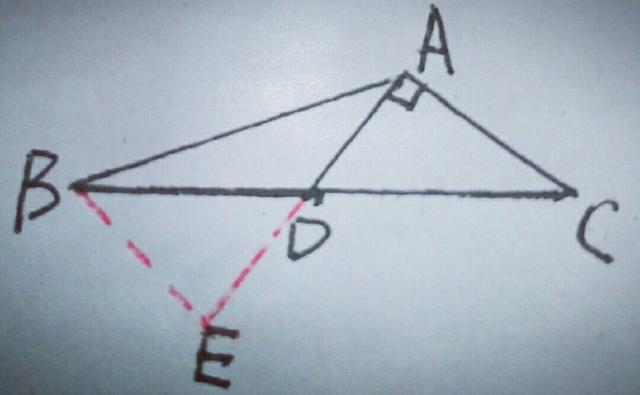
则BE=AB/2，∠BED=∠CAD=90°，又∠ADC=∠BDE，BD=DC，∴△BDE≌△CDA，∴AC=BE=AB/2.(本题因BD=DC，所以倍长中线也可证出)

【总结】辅助线往往来于定理或性质，或图形的完整补充，我们可以做一些难题，更重要的是，通过做题，归纳总结方法.