初中数学《轴对称》所有考点、易错点全在这里啦

一、知识框架

知识框架

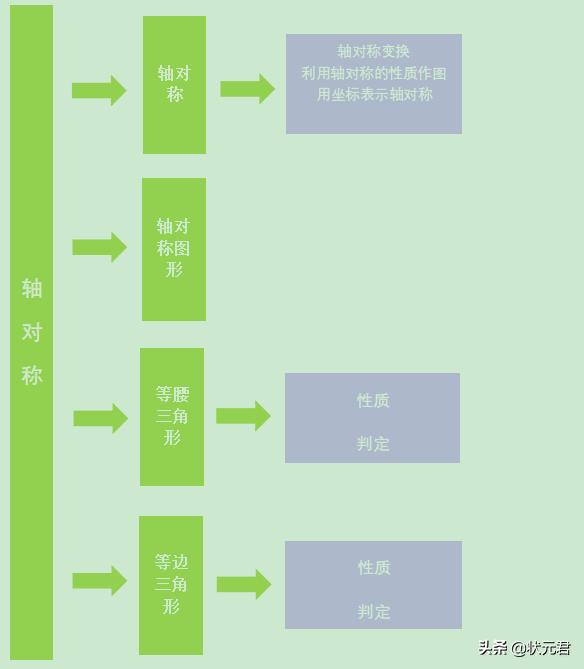
思考：你知道什么是轴对称吗？生活中有哪些轴对称图形呢？下列图片中有轴对称图形吗？如果有，它们的对称轴在哪里？尝试说出轴对称图形的特点。

二、知识梳理与拓展应用

（一）轴对称

1.轴对称图形

如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫作轴对称图形，这条直线就是它的对称轴.这时，我们也说这个图形关于这条直线(或轴)对称。

2.轴对称

把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫作对称轴，折叠后重合的点是对应点，叫作对称点。

拓展延伸：

两个图形成轴对称和轴对称图形的前提不一样，前者是两个图形，后者是一个图形，成轴对称的两个图形不仅大小、形状一样，而且与位置有关。

例1：如图1所示，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上，若PM＝2.5cm，PN＝3cm，MN＝4cm，则线段QR的长为（ ）cm。

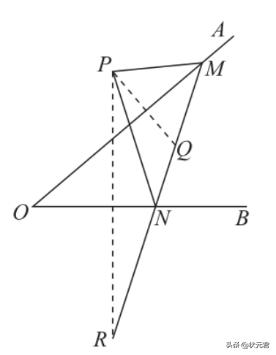
图1

A. 4.5

B. 5.5

C. 6.5

D. 7

解：因为点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上，

所以PM＝MQ，PN＝NR.

因为PM＝2.5cm，PN＝3cm，MN＝4cm,

所以NR＝3cm，MQ＝2.5cm，

即NQ＝MN－MQ＝4－2.5＝1.5(cm)，

则线段QR的长为RN+NQ＝3+1.5＝4.5(cm).

答案：A

3.垂直平分线

经过线段中点并且垂直于这条线段的直线，叫作这条线段的垂直平分线。

4.线段的垂直平分线的性质

(1)线段的垂直平分线上的点，到这条线段两个端点的距离相等。

(2)与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

5.轴对称和轴对称图形的性质

(1)如果两个图形关于某条直线对称，那么这条直线叫作对称轴，对称轴是两个图形中任何一对对应点所连线段的垂直平分线。

(2)轴对称图形的对称轴是轴对称图形中任何一对对应点所连线段的垂直平分线。

关键提醒：

轴对称图形(或关于某条直线对称的两个图形)，它们的对应线段相等，对应角相等。

6.轴对称的特征

如果一个图形关于某条直线对称，那么连接对称点的线段的垂直平分线就是该图形的对称轴。

（二）画轴对和图形

1.作图形的对称轴

找对称轴的方法:首先判断是不是轴对称图形，再观察是否存在一条直线将这个图形分成两部分，将这两部分沿这条直线折叠，如果重合，这条直线就是对称轴。另外，要全方位地去找，不要漏掉对称轴。

2.画轴对称图形

组成几何图形最基本的元素是“点”，所以画轴对称图形必须掌握对称点的画法(即过已知点作对称轴的垂线并加倍延长即可)。

画轴对称图形的步骤如下:

(1)确定对称轴；

(2)作各定点关于对称轴的对称点；

(3)按原图的形状依次连接各对称点。

例2：如图2所示，已知△ABC和直线l，试画出△ABC关于直线l的对称图形。

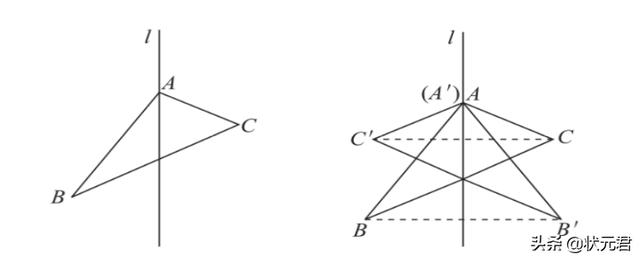
图2 图3

解析：分别作出A、B、C三点关于直线l的对称点A′、B′、C′，后顺次连接即可。

解：所画图形如图3所示:△A'B'C'即为所求。

3.用坐标表示轴对称

(1)已知点关于x轴或y轴对称的点的坐标的规律:

点(x，y)关于x轴对称的点的坐标为

(x，－y)；

点(x，y)关于y轴对称的点的坐标(－x， y)。

(2)如何在坐标系中作一个已知图形的对称图形:只要找到一些特殊点(如多边形的顶点)的对称点的坐标，描出并连接这些点，就可以得到这个图形的轴对称图形。

例3：在平面直角坐标系中，已知点A(2，3)，则点A关于x轴对称的点的坐标为( ).

A.(3，2)

B.(2，－3)

C.( －2， 3)

D.( －2，－3)

解析 因为点A(2，3)，所以点A关于x轴对称的点的坐标为(2，－3).

答案 B

（三）等腰三角形

1.等腰三角形

有两条边相等的三角形叫作等腰三角形.相等的两条边叫作腰，另条边叫作底边，两腰所夹的角叫作顶角，底边与腰的夹角叫作底角。

2.等腰三角形的性质

性质1:等腰三角形的两个底角相等(简写成“等边对等角”)。

性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称“三线合一”)。

性质3:等腰三角形是轴对称图形，底边的垂直平分线就是它的对称轴。

知识拓展：

等腰三角形是轴对称图形，其顶角的平分线、底边上的中线、底边上的高线所在的直线是对称轴。等腰三角形的外心、内心、重心和垂心都在底边的高线上(即“四心共线”)。等腰直角三角形的底角都等于45°。

关键提醒：

运用等腰三角形的性质解题时，在等腰三角形中若已知一内角为锐角，而未指明是底角还是顶角时，应注意分类讨论，防止漏解。

3.等腰三角形的判定方法

(1)利用定义:两条边相等的三角形是等腰三角形。

(2)如果一个三角形有两个角相等，那么这两个角所对的边也相等(简写成“等角对等边”)。

例4：如图4所示，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，∠A＝∠ABE。若AC＝5，BC＝3，则BD的长为( )。

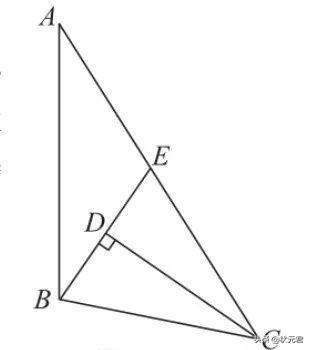
图4

解:如图4所示，因为CD平分∠ACB，BE⊥CD所以BC＝CE。又因为∠A＝∠ABE，所以AE＝BE。

所以BD＝BE＝AE＝(AC－BC)。

因为AC＝5，BC＝3,

所以BD＝1

答案D

（四）等边三角形

1.等边三角形

在等腰三角形中，有一种特殊的等腰三角形—三边都相等的三角形，我们把这样的三角形叫作等边三角形。

知识拓展：

由定义可知，等边三角形是一种特殊的等腰三角形，也就是说等腰三角形包括等边三角形，因而等边三角形具有等腰三角形的一切性质。

2.等边三角形的性质和判定方法

(1)性质：

①等边三角形的三个内角都相等，并且每一个角都等于60°。

②等边三角形是轴对称图形，它有三条对称轴。

(2)判定：

①三个角都相等的三角形是等边三角形。

②有一个角是60°的等腰三角形是等边三角形。

例5：如图5所示，等边△ABC的边长是6cm，BD是中线，延长BC至使CE＝CD，连接DE，则DE的长是（ ）cm。

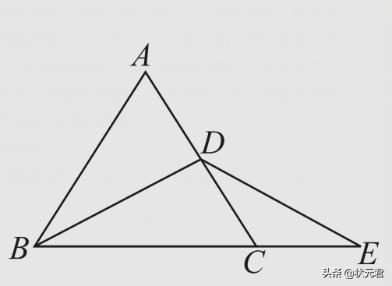
图5

解析：因为△ABC是等边三角形，BD是中线，所以∠ABC＝∠ACB＝60°，所以∠DBC＝30°。又因为CE＝CD，所以∠CDE＝∠CED.又因为∠BCD＝∠CDE+∠CED，所以∠CDE＝∠CED＝∠BCD＝30°。所以∠DBC＝∠CED，即DB＝DE。因为等边△ABC的边长是6cm，所以DE＝BD＝3cm。

（五）含30°角的直角三角形

在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

关键提醒：应用此性质的前提条件是“在直角三角形中”。

例6：如图6所示，△ABC中，∠C＝90°，AC＝3，∠B＝30°，点P是BC边上的动点，则AP长不可能是( )。

A.3.5

B.4.2

C.5.8

D.7

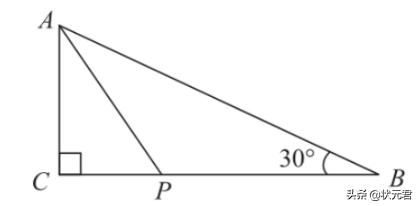
图6

解析：由垂线段最短可知，AP的长不可小于3.因为在△ABC中，∠C＝90°，AC＝3，∠B＝30°，所以AB＝6，所以AP的长不能大于6。故选D。

答案 D

思考：你理解轴对称的概念了吗？可以举出两个生活中轴对称图形的实例吗？