初中三角形最常见26种做辅助线做法及思路

1、在利用三角形三边关系证明线段不等关系时，如果不能直接证明结果，可以接连两点或延长一边构造三角形，使结论中出现的线段在一个或几个三角形中，然后利用三边关系定理及不等式性质证明。（注意：利用三角形三边关系定理及推论证明时，常通过做辅助线，将求证量或与求证相关的量移到同一个或几个三角形中）

2、利用三角形外角大于任何与它不相邻的内角证明角的不等关系式，可连接两点或延长某边，构造三角形，使求证的大角在某个三角形外角的位置上，小角处在内角的位置上，再利用外角定理证明。

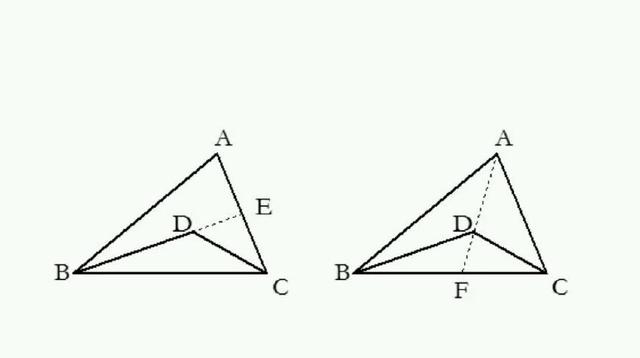
3、有角平分线时常在角两边截取相等的线段，构造全等三角形

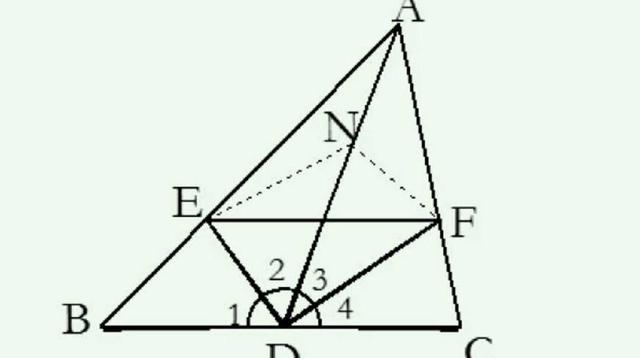
4、有线段中点为端点的线段时，常加倍延长此线段构造全等三角形

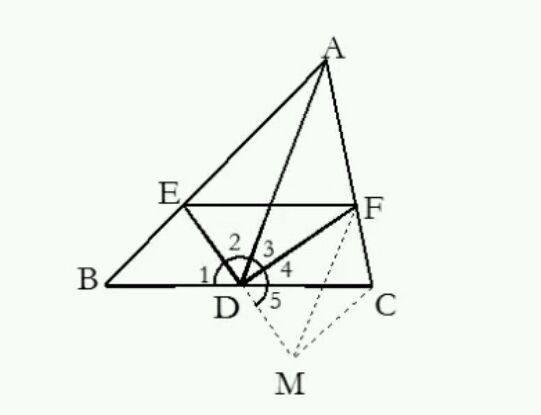
5、在三角形中有中线时，常加倍延长中线构造全等三角形

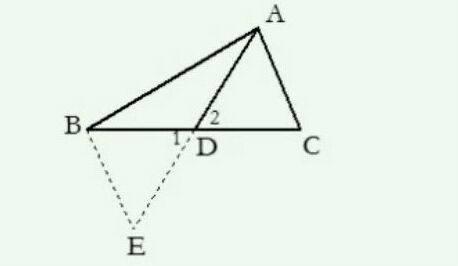
6、截长补短作辅助线的方法

截长法：在较长的线段上截取一条线段等于较短线段

补短法：延长较短线段和较长线段相等

7、证明两条线段相等的步骤：

①观察要证明线段在那两个可能全等的三角形中，然后证明这两个三角形全等；

②若图中没有全等三角形，可以把求证线段用和它相等的线段代替，再证明它们所在三角形的全等；

③如果没有相等的线段替换，可作辅助线构造全等三角形。

8、在一个图形中，有多组垂直关系时，常用同角（等角）的余角相等来证明两个角相等。

9、三角形一边的端点到这边的中线所在的直线的距离相等

10、条件不足时延长已知边构造三角形

11、连接四边形的对角线。把四边形问题转化成三角形来解决

12、有和角平分线垂直的线段时，通常把这条线段延长，可归纳为“角分垂等腰归”

13、当证题有困难时，可结合已知条件，把图形中的某两点连接起来构造全等三角形。

14、当证题中缺少线段相等条件时，可取某条线段中点，为证题提供条件。

15、有角平分线时，常过平分线上的点向角两边做垂线，利用角平分线上的点到角两边距离相等证明。

16、有等腰三角形时常用的辅助线：

①作顶角的平分线、底边中线、底边高线

②有底边中点时，常作底边中线

③将腰延长一倍，构造直角三角形解题

④常过一腰上的某一已知点做另一腰的平分线

⑤常过某一腰上的某一已知点作底边的平行线

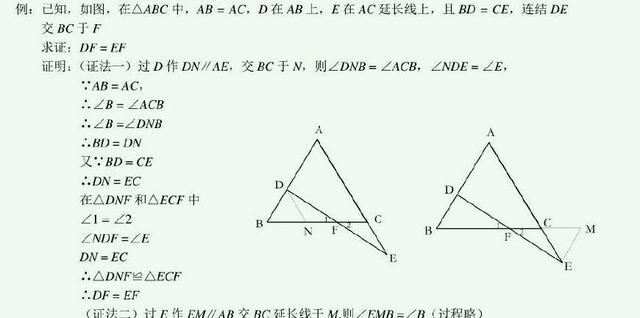
⑥常将等腰三角形转换成特殊等腰三角形――等边三角形

17、有二倍角时常用的辅助线:

①构造等腰三角形使二倍角是等腰三角形的顶角的外角

②平分二倍角

③加倍小角

18、有垂直平分线时常把垂直平分线抢的点与线段两端点连接起来

19、有垂直时长构造垂直平分线

20、有中点时常构造垂直平分线

21、当涉及到线段平分的关系时常构造直角三角形，利用勾股定理证题

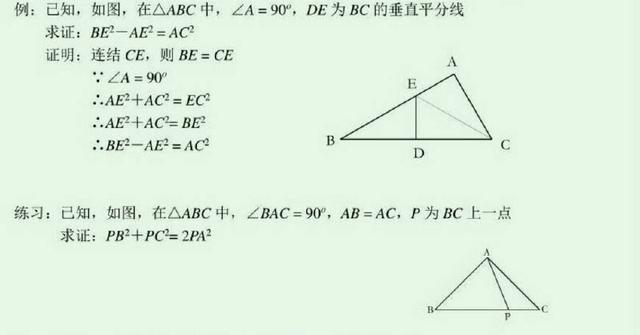
22、条件中出现特殊角时常做高把特殊角放在直角三角形中

23、三角形中一个内角平分线与一个外角平分线相交所称的锐角，等于第三个内角的一半

24、三角形中的两个内角平分线相交所成的钝角等于90°加上第三个内角的一半

25、三角形的两个外角平分线相交所成的锐角等于90°减去第三个内角的一半

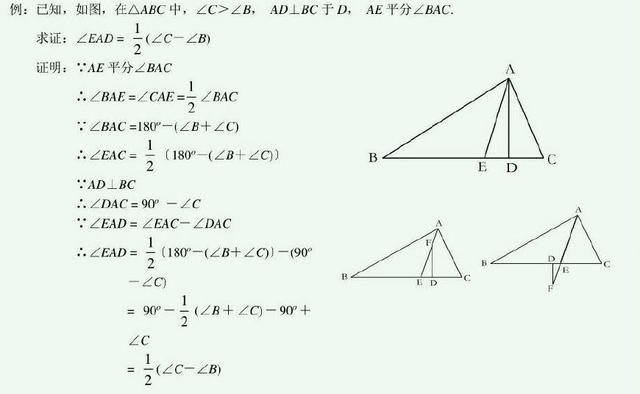
26、从三角形的一个顶点作高线和角平分线，它们所夹的角等于三角形另外两个角差的绝对值的一半