高考数学专题系列：—二元二次方程条件下的最值题型解法

一、 (ax＋by)(cx＋dy)=m最值问题

【举例】

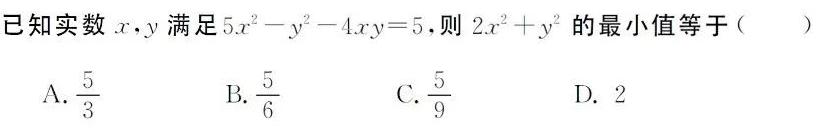
【解析】

一般地，若实数x、y满足(ax＋by)(cx＋dy) = m，其中a、b、c、d、m均为非零常数，要求关于实数x、y的二元二次式最值。

第一步：设ax＋by = t，cx＋dy = m/t，反解出x、y。

第二步：将x、y代入求得关于t的一元函数。

第三步：求这关于t的一元函数的最值。

上述方法同样适合求满足(ax＋by)(cx＋dy) = m的二元二次最值问题。

二、(ax+b)(cy+d)=m最值问题

【举例】

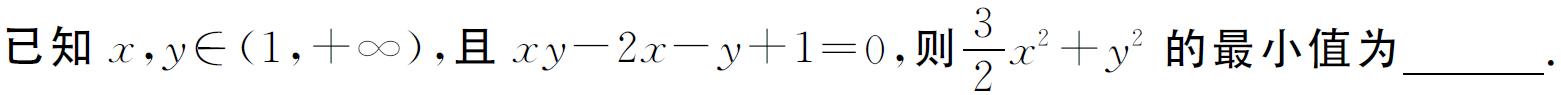
【解析】

本题可通过已知方程左边的因式进行局部换元，将二元最值问题转化为一元函数的最值问题来解。

一般地，若实数x、y满足(ax＋b)(cy＋d)=m，其中a、b、c、d、m均为非零常数，要求关于实数x、y的二元二次式最值。

第一步：设ax＋b = t，cy＋d = m/t，反解出x、y。

第二步：将x、y代入求得关于t的一元函数。

第三步：求这关于t的一元函数的最值。

上述方法同样适合求满足(ax＋b)(cx＋d)=m 的一元二次最值问题。

三、椭圆型方程下的二元最值问题

【举例】

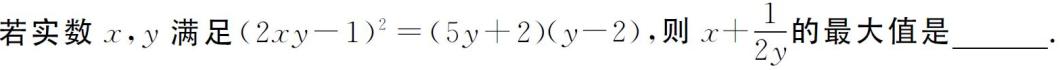
【解析】

椭圆型方程下的二元最值问题，通常用类似于椭圆的参数方程的方法进行三角换元，将问题转化为以角为变量的一元函数的最值问题求解。

本解法先对已知等式的变形和首次换元得出(2x－z)2+(2z＋1)2=9，这是接下来进行三角换元的关键。

四、二次方程条件下的一次最值问题

【举例】

【解析】

已知条件是关于x、y的二元二次方程，所求的是x、y的二元一次式的最值，通法是将所求一次式整体代换设为t，然后用消元法代入已知方程整理得关于另一个未知数的一元二次方程，最后用判别式法求出t的取值范围，验证等号成立求出最值。判别式法也适合已知三元二次方程求一次最值的问题。

五、求x2＋y2的最值问题

【举例】

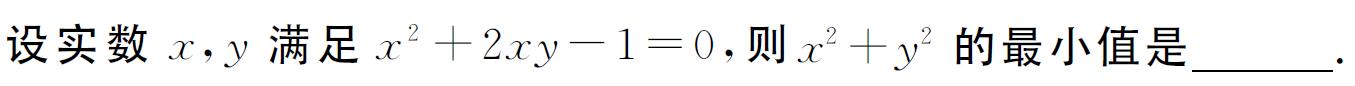
【解析】

上述解法从所求式子入手，注意到所求式子是平方和的形式，先整体换元设x2＋y2＝r2，再用圆的参数方程进行三角换元，然后用正弦函数的有界性求r2的最小值。