高考数学满分冲刺：巧用极点、极线——速解圆锥曲线压轴大题！

经典例题：

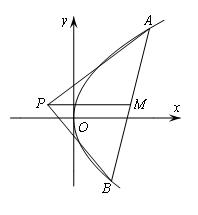
如图，已知点P是y轴左侧(不含y轴)一点，抛物线C：y2=4x上存在不同的两点A，B满足PA，PB的中点均在C上

(1)设AB中点为M，证明：PM垂直于y轴

(2)若P是半椭圆x2+y2/4=1(x<0)上的动点，求△PAB面积的取值范围

解析：

（1）设P（x0，y0）

（2）连CB,AD交于Q，由于AB∥CD过P作曲线C的两条切线PE，PF，切点为E，F。则P对应的极线为EF，显然EF过Q，且AB∥EF∥CD，

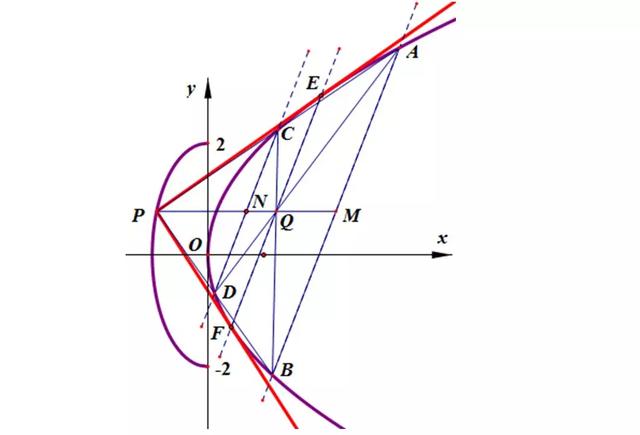
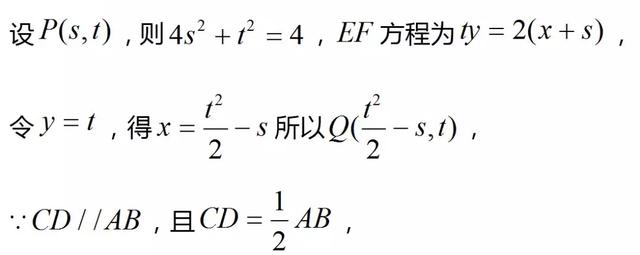
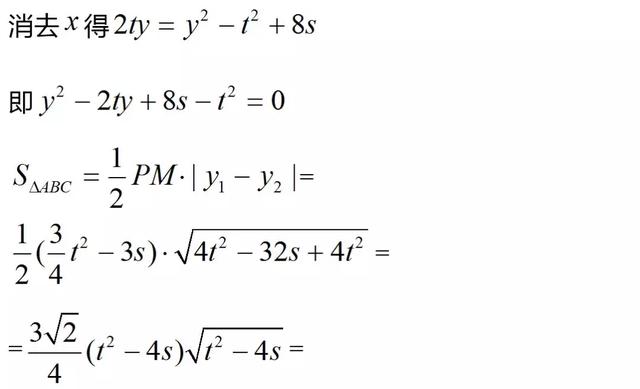
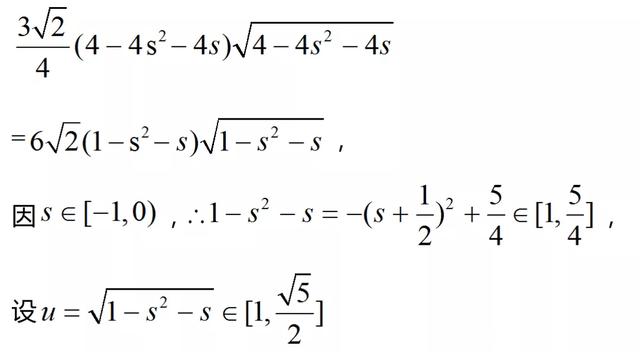
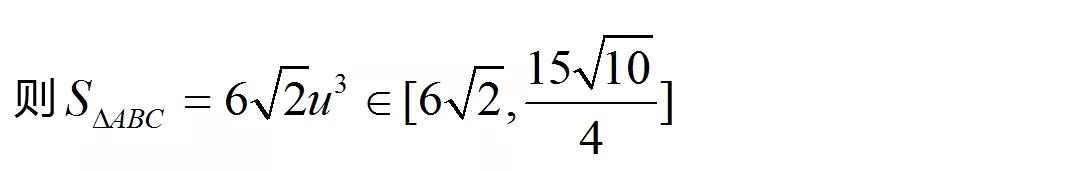
总结：圆锥曲线的两个端点和这两个端点处的切线的交点所构成的三角形叫阿基米德三角形，这条弦叫做阿基米德三角形的底，两长切线的交点叫阿基米德三角形的顶点。本题的极限情形之一为阿基米德三角形。