冲击19年中考数学，专题复习215：二次函数有关的应用题

典型例题分析1：

某服装商场经销一种品牌运动套装，已知这种品牌运动套装的成本价为每套300元，市场调查发现，这种品牌运动套装每天的销售量y（个）与销售单价x（元）有如下关系：y=﹣x+600（300≤x≤600）．设这种品牌运动套装每天的销售利润为w元．

（1）求w与x之间的函数关系式；

（2）这种品牌运动套装销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？

（3）如果物价部门规定这种品牌运动套装的销售单价不高于420元，该商店销售这种品牌运动套装每天要获得20000元的销售利润，销售单价应定为多少元？

解：（1）w=（x﹣300）（﹣x+600）=﹣x²+900x﹣180000；

（2）∵w=﹣x²+900x﹣180000=﹣（x﹣450）²+22500，

∴当x=450时，w有最大值，最大值为22500；

（3）当w=20000时，可得﹣x²+900x﹣180000=20000，

解得：x₁=400、x₂=500，

∵500＞420，

∴x=400，

答：该商店销售这种品牌运动套装每天要获得20000元的销售利润，销售单价应定为400元．

典型例题分析2：

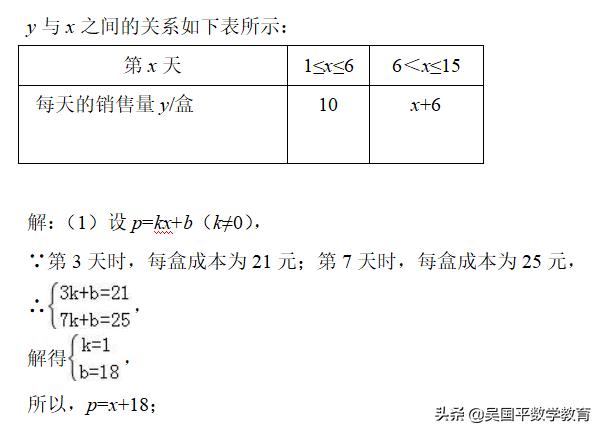
某市“荷花节”举办了为期15天的“荷花美食”厨艺秀．小张购进一批食材制作特色美食，每盒售价为50元，由于食材需要冷藏保存，导致成本逐日增加，第x天（1≤x≤15且x为整数）时每盒成本为p元，已知p与x之间满足一次函数关系；第3天时，每盒成本为21元；第7天时，每盒成本为25元，每天的销售量为y盒，（1）求p与x的函数关系式；

（2）若每天的销售利润为w元，求w与x的函数关系式，并求出第几天时当天的销售利润最大，最大销售利润是多少元？

（3）在“荷花美食”厨艺秀期间，共有多少天小张每天的销售利润不低于325元？请直接写出结果．

典型例题分析3：

近年以来，国务院连续发布了《关于加快构建大众创业万众创新支撑平台的指导意见》等一系列支持性政策，各地政府高度重视、积极响应，中国掀起了大众创业万众创新的新浪潮．某创新公司生产营销A、B两种新产品，根据市场调研，发现如下信息：

信息1：销售A种产品所获利润y（万元）与所售产品x（吨）之间存在二次函数关系y=ax²+bx，当x=1时，y=7；当x=2时，y=12．

信息2：销售B种产品所获利润y（万元）与所售产品x（吨）之间存在正比例函数关系y=2x．

根据以上信息，解答下列问题：

（1）求a，b的值；

（2）该公司准备生产营销A、B两种产品共10吨，请设计一个生产方案，使销售A、B两种产品获得的利润之和最大，最大利润是多少？

考点分析：

二次函数的应用．

题干分析：

（1）把两组数据代入二次函数解析式，然后利用待定系数法求解即可；

（2）设购进A产品m吨，购进B产品（10﹣m）吨，销售A、B两种产品获得的利润之和为W元，根据总利润等于两种产品的利润的和列式整理得到W与m的函数关系式，再根据二次函数的最值问题解答．