初中数学典型习题详解

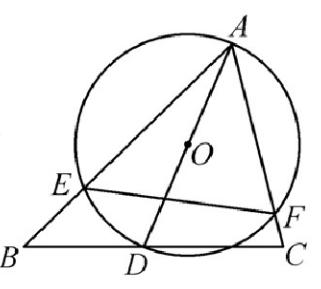
图1.1

1、如图1.1，在△ABC中，∠BAC=60°，∠ABC=45°，AB=2√2，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB、AC与点E、F，连接EF，求线段EF长度的最小值。

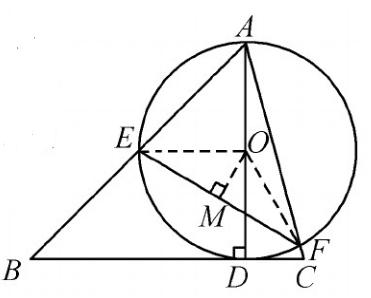
图1.2

解：如图1.2，连接OE、OF，过点O作OM⊥EF于点M，

则EM=FM=1/2EF，∴∠EOF=2∠BAC=120°，∴∠EOM=1/2∠EOF=60°，

∴EM/OE=sin60°=√3/2，∴EM=√3/2OE，∴EF=2EM=√3OE。

即当⊙O的半径最小时，线段EF的长最小。

∵当AD⊥BC时，直径AD最小，∴此时⊙O的半径最小。

在Rt△AOC中，sinB=AD/AB=√2/2，∴AD=√2/2AB=2，∴OE=1/2AD=1，

∴EF=√3OE=√3

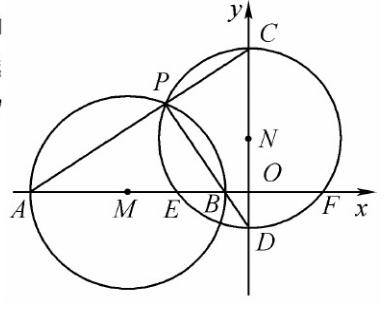
图2.1

2、如图2.1，以M（-5,0）为圆心，4为半径的圆与x轴交于A、B两点，P是⊙M上异于A、B的动点，直线PA、PB分别交y轴于C、D两点，以CD为直径的⊙N与x轴交于E、F两点，求EF的长。

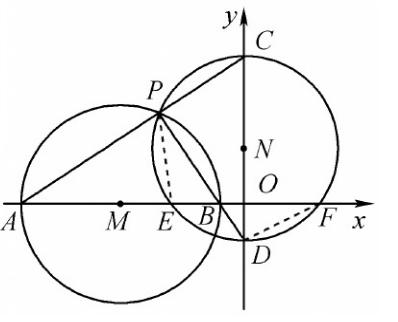
图2.2

解：∵∠APB=∠BOD=90°，∠PBA=∠OBD，

∴△BPA∽△BOD，∴OB/PB=BD/BA，

∵OB=1，BA=8，∴PB·BD=8

连接PE、DF，易得△EBP∽△DBF，

∴BE/BD=PB/FB，∴PB·BD=BE·FB=BE·(BE+1+1)=8，

∴BE²+2BE-8=0，∴BE=2或BE=-4（舍去）

∴EF=BF+FB=2+4=6

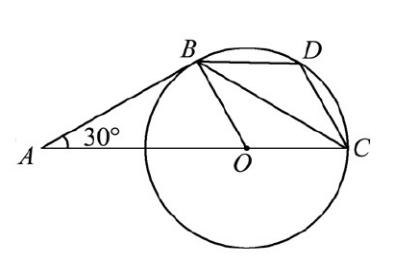
图3.1

3、如图3.1，AB是⊙O的切线，B是切点，圆心在AC上，∠A=30°，D位弧BC的中点。（1）证明：AB=BC.（2）四边形BOCD是菱形。

解：（1）∵AB是⊙O的切线，

∴∠OBA=90°，∠AOB=60°。

∵OB=OC，∴∠OBC=∠OCB

∵∠AOB=∠OBC+∠OCB，

∠OCB=∠A=30°，∴AB=AC

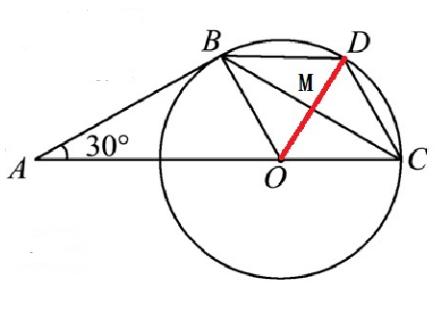
图3.2

（2）连接OD交BC于点M，

∵D是弧BC的中点，∴OD垂直平分BC。

在直角△OMC中，∵∠OCM=30°，∴OC=2OM=OD。

∴OM=DM，∴BC垂直平分OD。

∴四边形BOCD是菱形。