巧解初中几何题：怎样证明线段平方的和差关系

勾股定理揭示了直角三角形三边的平方关系，因此，对于证明线段平方的和、差关系类题型，可设法构造出直角三角形，然后利用勾股定理及等式的性质进行证明.

【典例1】

已知：如下图，D是△ABC边BC上一点，且CD^2=AC^2-AD^2.求证：AB^2-AC^2=BD^2-CD^2.

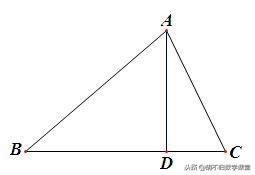
【思路分析】要证明结论成立，考虑由勾股定理得出和AB^2、AC^2相关的两个等式，再将两式相减即可.

【证明】在△ACD中，∵ CD^2=AC^2-AD^2， ∴ CD^2+AD^2=AC^2 ∴ ∠ADC=90°. 在Rt△ABD和Rt△ACD中，由勾股定理，得 AB^2=AD^2+BD^2，AC^2=AD^2+CD^2，两式相减，得AB^2-AC^2=BD^2-CD^2.

点评：本题难度不大，主要是从它身上得到启示——要证线段平方之间差的关系时，往往用勾股定理分别得出关于线段平方的关系式，然后再将两式相加或相减，并整理即可得出要证的等式.

【典例2】

已知：如下图所示，△ABC中，AB=AC，∠BAC=90°，D是BC上一点. 求证： BD^2+CD^2=2AD^2.

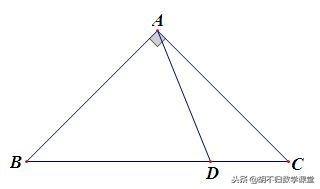
【思路分析】BD、CD、AD三条线段都不是直角三角形的边，故考虑引垂线构造直角三角形，若从点D引垂线，可使这三条线段都是直角三角形的边.

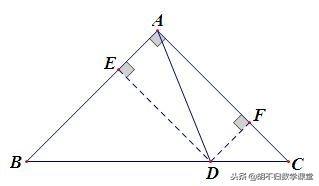
【证明】如上图，过点D分别作DE⊥AB于点E，DF⊥AC于点F，又 ∵ ∠BAC=90°，∴四边形AEDF是矩形，∴ AE=DF，DE=AF. ∵AB=AC，∠BAC=90°，∴ ∠B=∠C=45°. ∴ ∠BDE=45°.则∠B=∠BDE. ∴ BE=DE.

同理 CF=DF.

在Rt△BDE中， BD^2=BE^2+ED^2=2ED^2，在Rt△CDF中， CD^2=CF^2+DF^2=2DF^2.

∴ BD^2+CD^2=2（ED^2+DF^2）=2（ED^2+AE^2）=2AD^2.

【典例3】

已知：如下图所示，在四边形DBCE中，∠CBD+∠BCE=90°. 求证：DE^2+BC^2=BE^2+CD^2.

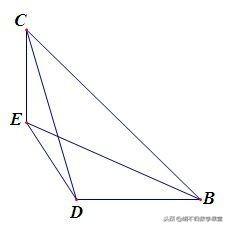
【思路分析】要证明结论成立，可将四条线段变成直角三角形的边，注意到条件∠CBD+∠BCE=90°，若把∠CBD、∠BCE看成一个三角形的两个角，这两个锐角互余，则第三个角必是直角. 故延长BD、CE相交于点A，则△ABC是直角三角形. 由勾股定理的得出相关等式，再将它们进行整理即可.

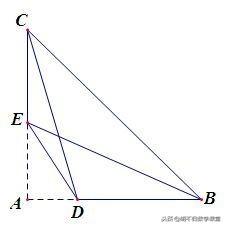
【证明】如上图，延长BD、CE相交于点A. ∵ ∠CBD+∠BCE=90°，∴ ∠A=90°. 在Rt△ADE中，DE^2=AD^2+AE^2. 在Rt△ABC中， BC^2=AB^2+AC^2.

∴ DE^2+ BC^2=AD^2+AE^2+AB^2+AC^2 . 在Rt△ABE中， BE^2=AE^2+AB^2 .

在Rt△ACD中， CD^2=AD^2+AC^2 . ∴ BE^2+ CD^2=AD^2+AE^2+AB^2+AC^2 .

∴ DE^2+BC^2=BE^2+CD^2.

本题带给我们的启示：若直接证某两个量相等有困难时，可以采用间接的方法，先证这两个量都等于第三个量，那么要证的这两个量就相等了.

【典例4】

已知：如下图所示，在四边形ABCD中，∠ABC=30°，∠ADC=60°，AD=DC. 求证：BD^2=AB^2+BC^2.

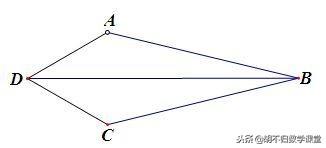
【思路分析】因为要证的结论与勾股定理的形式完全相同，因此，要证结论成立，考虑将BD、AB、BC三条线段转化为一个直角三角形的三条边.

【证明】如下图，连接AC. ∵ ∠ADC=60°，AD=DC，∴ △ADC是等边三角形. ∴ CD=CA，∠ACD=60°.

过点B作AB的垂线，并在上面截取BE=BC，连接AE、CE. ∵ ∠EBA=90°，∠ABC=30°，∴ ∠CBE=60°.

∵ BE=BC，∴ △BCE是等边三角形. ∴CB=CE，∠BCE=60°. 又∵∠ADC=60°，∴ ∠DCB=∠ACE. 则可得

△DCB≌△ACE（SAS）. ∴ BD=AE. 在Rt△ABE中，由勾股定理得AE^2=AB^2+BE^2.

∵ BD=AE， BE=BC，∴ BD^2=AB^2+BC^2.

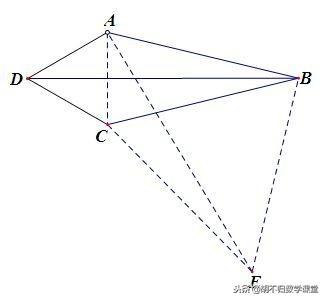
点评：①有两边相等，且其夹角为60°，一般都需要连接这两边构造出等边三角形；②若要证的线段的平方关系与勾股定理的结论从形式上相同，一般需要通过作辅助线，将三条线段集中到同一个直角三角形中，再由勾股定理进行证明.