高考数学：函数的奇偶性模型快速解题规律归纳！

判断函数奇偶性的步骤

(1)求函数的定义域；

(2)判断定义域是否关于原点对称，若不对称，则函数为非奇非偶函数，若对称，则进行下一步；

(3)判断f(-x)与f(x)的关系，若f(-x)=f(x),则函数f(x)为偶函数，若f(-x)=-f(x),则函数f(x)为奇函数，若f(-x)≠±f(x),则f(x)为非奇非偶函数；

(4)得出结论.

函数奇偶性的几个重要快速解题结论

1.f(x)为奇函数⇔f(x)的图象关于原点对称；f(x)为偶函数⇔f(x)的图象关于y轴对称.

2.如果函数f(x)是偶函数，那么f(x)=f(|x|).

3.既是奇函数又是偶函数的函数只有一种类型，即f(x)=0,x∈D,其中定义域D是关于原点对称的非空数集.

4.奇函数在两个对称的区间上具有相同的单调性，偶函数在两个对称的区间上具有相反的单调性.

5.偶函数在关于原点对称的区间上有相同的最大(小)值，取最值时的自变量互为相反数；奇函数在关于原点对称的区间上的最值互为相反数，取最值时的自变量也互为相反数.

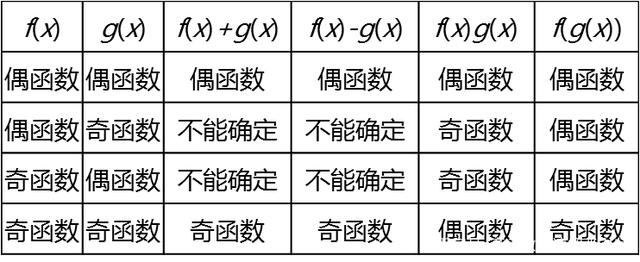
重要类型的奇偶函数

经典例题[2018全国卷]

答案：D

总结：1.在用定义判断函数的奇偶性时，要注意自变量在定义域内的任意性.不能因为个别值满足f(-x)=±f(x),就确定函数的奇偶性.2.判定分段函数奇偶性时要分段讨论f(-x)与f(x)的关系，只有当所有区间上都满足相同的关系时，才能判定其奇偶性.3.在求出定义域之前，不能化简函数解析式，否则会使定义域发生变化.