高考数学：立体几何空间中的平行与垂直关系证明模板！

第一步，通过三角形的中位线、平行四边形寻找线线平行或线线垂直。

第二步，通过线线垂直或平行，利用判定定理，找线面垂直或平行，也可由面面关系的性质找线面垂直或平行。第三步，通过面面关系的判定定理，寻找面面垂直或平行。

第四步，严格按照定理中的条件规范书写解题步骤。

经典例题：

如图，AB是圆O的直径，C是圆O上异于A，B的一个动点，DC垂直于圆O所在的平面，DC∥EB，DC=EB=1，AB=4。

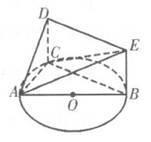
求证：DE⊥平面ACD：

思路分析：由已知条件证明DC⊥BC，AC⊥BC→BC⊥平面ACD．DC∥EB、DC=EB→BCDE→DE∥BC→DE⊥平面ACD。

总结：直线和平面平行首先是利用其判定定理，或者利用面面平行的性质来证，注意线线平行、线面平行、面面平行的转化；有中点时寻找中位线，利用三角形的中位线平行于底边、平行日边形的对边平行等有关性质。

当直线的方向向量与平面的法向量垂直时，直线和平面平行，但要注意指出直线不在平面内.