活用两个对称性，破解二次函数背景下的线段和最小值难题

在近几年的中考中，经常遇到求PA+PB最小型问题，为了让同学们对这类问题有一个比较全面的认识和了解，下面我们讲一下最常见的二次函数背景下的线段和最小值问题，希望对同学们有所帮助．

解题思路：找点关于线的对称点，实现"折"转"直"。

常用解题模型：在直线L上的同侧有两个点A、B，在直线L上有到A、B的距离之和最短的点存在，可以通过轴对称来确定，即作出其中一点关于直线L的对称点，对称点与另一点的连线与直线L的交点就是所要找的点．

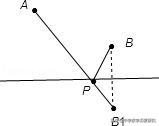
凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合本节所学轴对称变换来解决，多数情况要作点关于某直线的对称点．

例1．（2018秋•巴南区校级月考）如图抛物线y＝x²+2x﹣3与x轴交于A、B两点，与y轴交于点C，点P是抛物线对称轴上任意一点，若点D、E、F分别是BC、BP、PC的中点，连接DE，DF，则DE+DF的最小值为______．

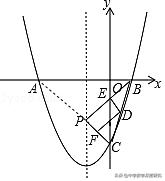
【分析】先确定抛物线的对称轴为直线x＝﹣1，C（0，﹣3），通过解方程x2+2x﹣3＝0得A（﹣3，0），B（1，0），再根据三角形中位线性质得DE＝1/2PC，DF＝1/2PB，所以DE+DF＝1/2（PC+PB），连接AC交直线x＝﹣1于P，如图，利用两点之间线段最短得到此时PB+PC的值最小，其最小值为AC的长，从而得到DE+DF的最小值．

【解答】：抛物线的对称轴为直线x＝﹣1，

当x＝0时，y＝x²+2x﹣3＝﹣3，则C（0，﹣3），

当y＝0时，x²+2x﹣3＝0，解得x1＝﹣3，x2＝1，则A（﹣3，0），B（1，0），

∵点D、E、F分别是BC、BP、PC的中点，∴DE和DF都为△PBC的中位线，

∴DE＝1/2PC，DF＝1/2PB，∴DE+DF＝1/2（PC+PB），

连接AC交直线x＝﹣1于P，如图，

∵PA＝PB，∴PB+PC＝PA+PC＝AC，

∴此时PB+PC的值最小，其最小值为3√2，∴DE+DF的最小值为3√2/2．

故答案为3√2/2．

【点评】本题考查了抛物线与x轴的交点：把求二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解关于x的一元二次方程．也考查了二次函数的性质和最短路径问题．

变式练习1．（2018•碑林区校级三模）如图，抛物线y＝﹣x²+2x+3交x轴于A，B两点，交y轴于点C，点C关于抛物线的对称轴的对称点为E，点G，F分别在x轴和y轴上，则四边形EDFG周长的最小值为 ．

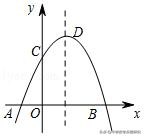
【答案】√2+√58．

提示：根据抛物线解析式求得点D（1，4）、点E（2，3），作点D关于y轴的对称点D′（﹣1，4）、作点E关于x轴的对称点E′（2，﹣3），从而得四边形EDFG的周长＝DE+DF+FG+GE＝DE+D′F+FG+GE′，当点D′、F、G、E′四点共线时，周长最短，据此根据两点间的距离公式可得答案．

例2．如图，抛物线y＝﹣x²﹣2x+3与x轴交于A、B两点，与y轴交于C点，M点在抛物线的对称轴上，当点M到点B的距离与到点C的距离之和最小时，点M的坐标为_____--

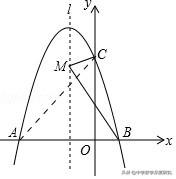
【分析】因为点A关于对称轴的对称点为点B，连接AC，设直线AC与对称轴x＝﹣1的交点为M，则此时MB+MC的值最小，再求得点M的坐标即可．

【解答】：∵抛物线y＝﹣x²﹣2x+3与x轴交于A、B两点，

∴点A（﹣3，0），C（0，3）

设直线AC的解析式为y＝kx+b，

∴把A（﹣3，0）、C（0，3）分别代入直线y＝kx+b，得-3k+b=0,c=3，

解得k=1,c=3，

∴直线AC解析式为y＝x+3；

设直线AC与对称轴x＝﹣1的交点为M，则此时MB+MC的值最小．

把x＝﹣1代入直线y＝x+3得，y＝2，

∴M（﹣1，2）．

即当点M到点A的距离与到点C的距离之和最小时M的坐标为（﹣1，2），

故答案为：（﹣1，2）．

【点评】本题考查了抛物线与x轴的交点问题，轴对称﹣最短路线问题，求得直线AC的解析式是解题的关键．

变式练习2．（2018秋•广水市期中）如图，已知：二次函数y＝x²+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣3，0），与y轴交于点C，点D（﹣2，﹣3）在抛物线上．

（1）求抛物线的表达式；

（2）抛物线的对称轴上有一动点P，求出PA+PD的最小值；

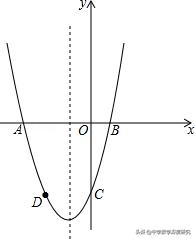
【答案】抛物线的表达式为y＝x²+2x﹣3；PA+PD的最小值为3√2．

提示：（1）由点A，D的坐标，利用待定系数法即可求出抛物线的表达式；

（2）利用二次函数图象上点的坐标特征可求出点B的坐标，连接BD，交抛物线的对称轴于点P，由抛物线的对称性及两点之间线段最短可得出此时PA+PD取最小值，最小值为线段BD的长度，再由点B，D的坐标，利用两点间的距离公式可求出PA+PD的最小值；

变式练习3．（2018秋•市南区校级月考）如图，已知：二次函数y＝x²+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣3，0），与y轴交于点C（0，﹣3）在抛物线上．

（1）求抛物线的表达式；

（2）抛物线的对称轴上有一动点P，求出当PB+PC最小时点P的坐标；

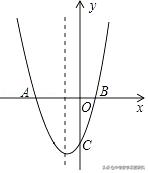
【答案】抛物线的解析式为y＝x²+2x﹣3；点P的坐标为（﹣1，﹣2）

提示：（1）根据题目中点A和点C的坐标可以求得该抛物线的解析式；

（2）根据二次函数图象具有对称性和两点之间线段最短可以求得点P的坐标；

变式练习4．（2018秋•庐阳区校级月考）如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0）

（1）求抛物线的解析式和对称轴；

（2）在抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；

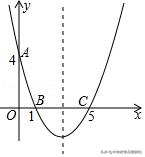
【答案】(1)抛物线解析式为y＝4/5（x﹣1）（x﹣5）＝4/5x²﹣24x/5+4．

抛物线对称轴x＝3．(2)交点P为（3，8/5）；

提示：（1）因为抛物线经过点B（1，0），C（5，0），可以假设抛物解析式为y＝a（x﹣1）（x﹣5），把A（0，4）代入即可解决问题，对称轴根据图象即可解决．（2）连接AC与对称轴的交点即为点P，此时△PAB周长最小．求出直线AC的解析式即可解决问题；

例3．（2018秋•微山县期中）如图，抛物线y＝ax2+bx+c与x轴交于A，B（1，0）两点，与y轴交于点C，直线y＝1/2 x﹣2经过A，C两点，抛物线的顶点为D．

（1）求抛物线的解析式及顶点D的坐标；

（2）在直线AC上方的抛物线上存在一点P，使△PAC的面积最大，请直接写出P点坐标及△PAC面积的最大值；

（3）在y轴上是否存在一点G，使得GD+GB的值最小？若存在，求出点G的坐标；若不存在，请说明理由．

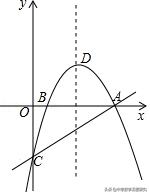
【分析】（1）利用一次函数是性质求得点A、C的坐标，然后把点A、B、C的坐标分别代入二次函数解析式，利用待定系数法求得二次函数解析式即可；将二次函数解析式转化为顶点式方程，可以直接得到答案；

（2）利用分割法求得△PAC的面积为二次函数的形式，利用二次函数最值的求法进行解答；

（3）利用轴对称﹣最短路径方法证得点G，结合一次函数图象上点的坐标特征求得点G的坐标．

【解答】：（1）把x＝0代入y＝1/2x﹣2中得：y＝﹣2．

把y＝0代入y＝1/2x﹣2中得：x＝4．∴A（4，0），C（0，﹣2）．

把A（4，0），B（1，0），C（0，﹣2）分别代入y＝ax2+bx+c，

得16a+4b+c=0,a+b+c=0,c=-2,

解得a=-1/2,b=5/2,c=-2．

则该抛物线的解析式为：y＝﹣1/2x2+5/2x﹣2，

∴y＝﹣1/2x²+5x/2﹣2＝﹣1/2（x﹣5/2）²+9/8，∴顶点D（5/2，9/8）；

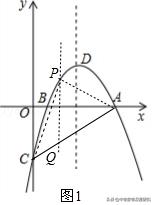
（2）在直线AC的上方抛物线上存在点P（2，1），使△PAC的面积最大，最大值为4．理由如下：如图1，过点P作PQ∥y轴交AC于Q，连接PC，PA．

设P（x，﹣1/2x²+5x/2﹣2），则Q（x，1/2x﹣2）．

∴PQ＝﹣1/2x²+5x/2﹣2﹣（1/2x﹣2）＝﹣1/2x²+2x＝﹣1/2（x﹣2）²+2．

又∵S△PAC＝S△PQC+S△PQA＝1/2x•PQ+1/2（4﹣x）•PQ＝2PQ，

∴S△PAC＝﹣（x﹣2）²+4．

∴当x＝2时，S△PAC最大值为4，此时﹣1/2x²+5x/2﹣2＝1，

∴在直线AC的上方抛物线上存在点P（2，1），

使△PAC的面积最大，最大值为4；

（3）存在点G（0，9/28）使得GD+GB的值最小．

理由如下：如图1，作点B关于y轴的对称点B′，连接B′D交y轴于点G，则B′（﹣1，0）．设直线B′D的解析式为y＝kx+b．

则5/2k+b=9/8, -k+b=0，解得：k=9/28,b=9/28．

∴直线B′D的解析式为y＝9/28x+9/28，

把x＝0代入，得y＝9/28，

∴存在点G（0，9/28）使得GD+GB的值最小．

【点评】本题是二次函数综合题、一次函数的应用，轴对称、待定系数法等知识，解题的关键是，学会利用参数构建方程解决问题，学会用数形结合的思想思考问题，属于中考压轴题．

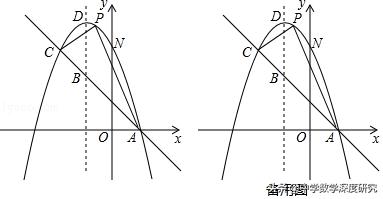
变式练习5．（2018秋•泰山区期中）如图，已知抛物线y＝﹣x²+bx+c与一直线相交于A（1，0）、C（﹣2，3）两点，与y轴交于点N，其顶点为D．

（1）求抛物线及直线AC的函数关系式；

（2）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P的坐标；

（3）在对称轴上是否存在一点M，使△ANM的周长最小．若存在，请求出M点的坐标和△ANM周长的最小值；若不存在，请说明理由．

【答案】(1)抛物线的函数关系式为y＝﹣x²﹣2x+3；

直线AC的函数关系式为y＝﹣x+1．

(2)△APC的面积取最大值，最大值为27/8，此时点P的坐标为（﹣1/2，15/4）．

(3)在对称轴上存在一点M（﹣1，2），使△ANM的周长最小，△ANM周长的最小值为3√2+√10．

提示：（1）根据点A，C的坐标，利用待定系数法即可求出抛物线及直线AC的函数关系式；

（2）过点P作PE∥y轴交x轴于点E，交直线AC于点F，过点C作CQ∥y轴交x轴于点Q，设点P的坐标为（x，﹣x²﹣2x+3）（﹣2＜x＜1），则点E的坐标为（x，0），点F的坐标为（x，﹣x+1），进而可得出PF的值，由点C的坐标可得出点Q的坐标，进而可得出AQ的值，利用三角形的面积公式可得出S△APC＝﹣3/2x²﹣3x/2+3，再利用二次函数的性质，即可解决最值问题；

（3）利用二次函数图象上点的坐标特征可得出点N的坐标，利用配方法可找出抛物线的对称轴，由点C，N的坐标可得出点C，N关于抛物线的对称轴对称，令直线AC与抛物线的对称轴的交点为点M，则此时△ANM周长取最小值，再利用一次函数图象上点的坐标特征求出点M的坐标，以及利用两点间的距离公式结合三角形的周长公式求出△ANM周长的最小值即可得出结论．

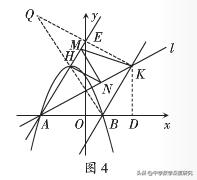
点评：求解长度和最值问题的关键点在于作"对称"，将"双动点问题"转化为"单一动点"。其解题思路是充分利用数形结合思想，动中取静，先将其中一个动点当做定点，将问题转化为单动点型问题，逐步求解。通过两次对称点转化把这三个距离转化到同一条直线上，根据两点之间线段最短求出最值。

综上所述可知：涉及最短距离的问题一般要考虑线段的性质定理，结合抛物线的轴对称变换（最短距离模型）来解决，多数情况要作某点关于对称轴的对称点。

解这类问题的关键在于：要注意结合轴对称的性质和线段垂直平分线的性质，以及有关线段大小关系的定理或公理，如"两点之间线段最短"，"三角形两边之和大于第三边"等。