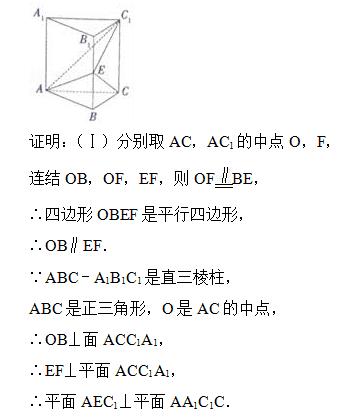
如图,在直三棱柱ABC﹣A1B1C1中,△ABC是正三角形,E是棱BB1的中点.
(Ⅰ)求证平面AEC1⊥平面AA1C1C;
(Ⅱ)若AA1=AB,求二面角C﹣AE﹣C1的平面角的余弦值.

考点分析:
二面角的平面角及求法;平面与平面垂直的判定。
两个平面垂直,则一个平面内垂直于交线的直线垂直于另一个平面。
在证明两平面垂直时,一般先从现有的直线中寻找平面的垂线,若这样的直线图中不存在,则可通过作辅助线来解决,如有平面垂直时,一般要用性质定理。
题干分析:
(Ⅰ)分别取AC,AC1的中点O,F,推导出四边形OBEF是平行四边形,从而OB∥EF.推导出OB⊥面ACC1A1,从而EF⊥平面ACC1A1,由此能证明平面AEC1⊥平面AA1C1C.
(Ⅱ)建立空间直角坐标系,利用向量法能求出二面角C﹣AE﹣C1的平面角的余弦值.

 加载中,请稍侯......
加载中,请稍侯......
精彩评论