RT三角形要求证不相关的两条边倍数关系（附所有几何证明题方法）

考试题目(5分)

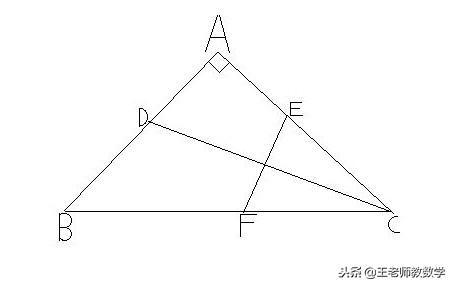
在△ABC中,∠A=90°,AB=AC,点D,E,F分别在边AB,AC,BC上,且AD=AE 如下图,在△ABC中,∠A=90°,AB=AC,点D、E、F分别在边AB、AC、BC上，且AD＝AE，CD垂直平分EF。求证：BF=2AD

做几何证明题的方法：我们要用综合法和分析法两头凑。

综合法：我们要求把所有已知条件标注在图上，同时把根据已知条件能得出的所有结论也全标注在图里面.一目了然。

分析法：把需要证明的去倒推，缺什么补什么，到哪里去补？就到图上标注的已经条件去找依据

最后两边凑，解答题目容易得多。

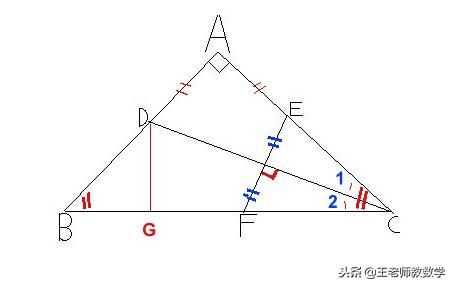
只要在几何里出现直角三角形并证明 : 一条边是另外一条边的倍数关系，或者一条边的平方等于另外一条或两条边的平方，而这些边又毫不相干的情况,那么我们必须要画辅助线，让这条辅助线成为要证明那两条线倍数关系的桥梁，或者把不相关的线放在同一个RT三角形里。