八年级经典几何题4，重在分析引出辅助线

【题目呈现】

题目一

【思路分析】

看题时，先通读一遍，统观全局，再看第二遍，叫细致入微，同时，各个击破，接下来，书写步骤，为之水到渠成。条件向结论靠，结论向条件走，相遇之后即成功.①求BE的长，应在Rt△ABE中，由勾股定理求得，而CF=EF=2，∴CE=CD=AB=4，而AE=3，∴BE可求.

②要证∠CEG=1/2∠AGE，有两个思路考虑:1，把∠AGE平分，这样过G点作GM⊥AE于M，如图，

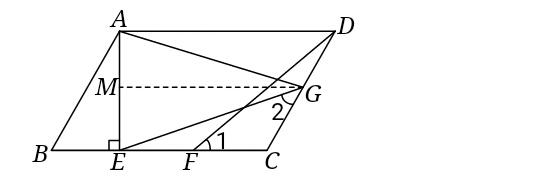
∵AE⊥BC，∴GM∥BC，∴∠CEG=∠EGM，接下来要证∠AGM=∠EGM，须证M为AE的中点或AG=EG，这时侯停下来再看条件，显然有∠1=∠2，∠C作公共角，CE=CD，∴△GCE≌△FCD，∴CG=CF=1/2CE=1/2CD，即G为CD的中点，∵GM∥BC，∴M为AE的中点，至此就已突破了该题。

2，虽然可考虑加倍∠CEG，但在图中加较麻烦，当证出G是CD的中点时，立马想到:"中线倍长"或"直角三角形斜边的中线等于斜边的一半”。于是有了辅助线，如图，

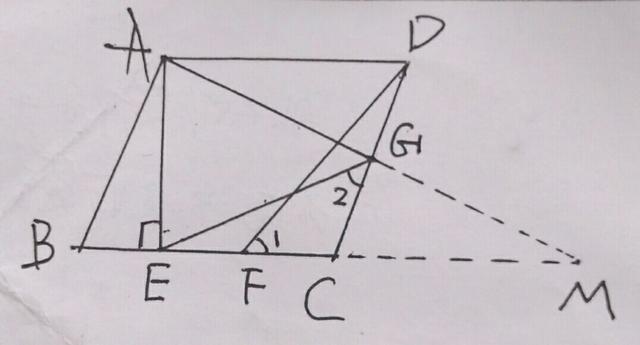
延长AG交EC的延长线于M，则AG=EG=MG，利用三角形外角的性质，

∠AGE=∠CEG+∠CMG，而∠CEG=∠CMG，∴∠CEG=1/2∠AGE.下面以第一种思路写一下步骤。

【步骤】

解:(1)∵CE=CD，CE=2CF，∴CD=2CF=2×2=4，∵四边形ABCD是平行四边形，∴AB=CD=4，而AE⊥BC，∴∠AEB=90°，在Rt△AEB中，由勾股定理得，BE²+AE²=AB²，∴BE=√7.

(2)证明:过点G作GM⊥AE于M，垂足为M，∵BC⊥AE，∴GM∥BC∥AD，又∠1=∠2，∠C=∠C，CE=CD，∴△ECG≌△DCF，∴CF=CG，又CE=CD，CF=1/2CE，∴CG=1/2CD，又∵GM∥BC∥AD，∴MG是直角梯形CEAD的中位线，所以M为AE的中点，又∵GM⊥AE，∴△AGE为等腰三角形，∴GM为∠AGE的角平分线，∴∠MGE=1/2∠AGE，∵GM∥BC，∴∠MGE=∠CEG，∴∠CEG=1/2∠AGE.

对应练习一

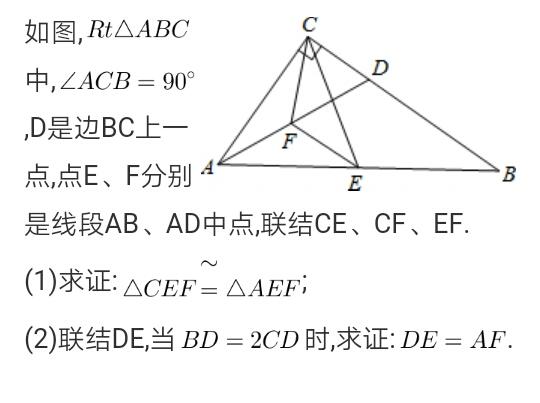
对应练习二

如图，在四边形ABCD中，∠ABC=90°，AC=AD，M、N分别为AC、CD的中点，连接BM、MN、BN.

(1)求证:BM=MN;

(2)若∠BAD=60°，AC平分∠BAD，AC=2，求BN的长.

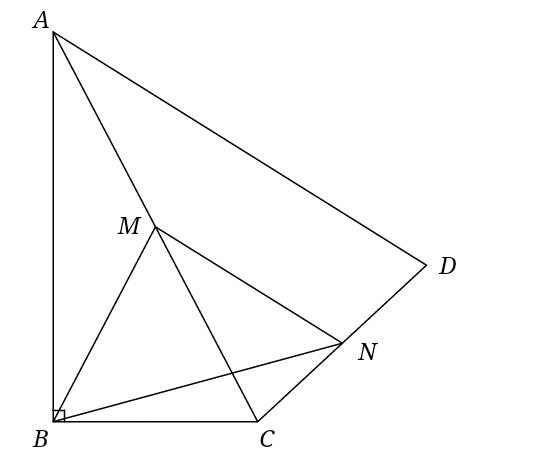
【答案:BN长为√2】

【总结反思】

虽然方法多种多样，但万变不离其宗。学会从给定条件，联系相关知识，引出辅助线，靠拢结论，当量变到质变时，能力自然就提高。