高考数学，典型例题分析210：圆有关的高考综合题

典型例题分析1：

几何证明选讲如图，已知AD为圆O的直径，直线BA与圆O相切于点A，直线OB与弦AC垂直并相交于点G，与弧AC相交于M，连接DC，AB=10，AC=12．

（1）求证：BA•DC=GC•AD；

（2）求BM．

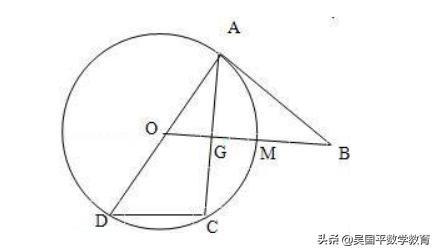
（1）证明：因为AC⊥OB，所以∠AGB=90°

又AD是圆O的直径，所以∠DCA=90°

又因为∠BAG=∠ADC（弦切角等于同弧所对圆周角）

所以Rt△AGB和Rt△DCA相似

所以BA/AD=AG/DC

又因为OG⊥AC，所以GC=AG

所以BA/AD=GC/DC，即BA•DC=GC•AD

（2）解：因为AC=12，所以AG=6，

因为AB=10，所以BG=8

由（1）知：Rt△AGB～Rt△DCA．

所以AB/AD=BG/AC

所以AD=15，即圆的直径2r=15

又因为AB²=BM•（BM+2r），即BM²+15BM﹣100=0

解得BM=5．

考点分析：

与圆有关的比例线段．

题干分析：

（1）根据AC⊥OB，及AD是圆O的直径，得到Rt△AGB和Rt△DCA相似，从而得到BA/AD=AG/DC，又GC=AG，所以BA/AD=GC/DC，从而得到证明；

（2）根据直角三角形中的边角关系求得BG，再根据直角三角形的相似及切割线定理求解即可．

典型例题分析2：

已知点A是直角三角形ABC的直角顶点，且A（2a，2），B（﹣4，a），C（2a+2，2），则△ABC的外接圆的方程是（ ）

A．x²+（y﹣3）²=5

B．x²+（y+3）²=5

C．（x﹣3）²+y²=5

D．（x+3）²+y²=5

解：由题意，2a=﹣4，

∴a=﹣2

∴圆的半径为BC/2=√5，圆心为（﹣3，0）

∴圆的方程为（x+3）²+y²=5

故选D．

考点分析：

圆的标准方程．

题干分析：

根据点A是直角三角形ABC的直角顶点，求出a，B，C的坐标求得圆心的坐标和圆的半径，则圆的方程可得．

典型例题分析3：

如图，圆O的弦AB，MN交于点C，且A为弧MN的中点，点D在弧BM上，若∠ACN=3∠ADB，求∠ADB的度数．

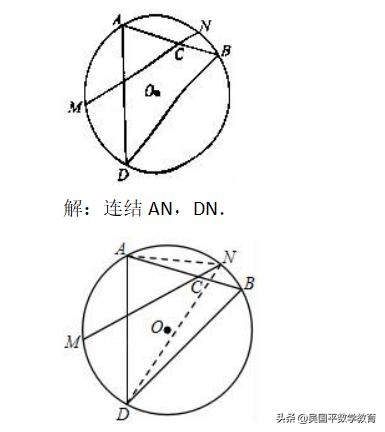
因为A为弧MN的中点，所以∠ANM=∠ADN．

而∠NAB=∠NDB，

所以∠ANM+∠NAB=∠ADN+∠NDB，

即∠BCN=∠ADB．

又因为∠ACN=3∠ADB，

所以∠ACN+∠BCN=3∠ADB+∠ADB=180°，

故∠ADB=45°．

考点分析：

弦切角．

题干分析;

结AN，DN．利用圆周角定理，结合∠ACN=3∠ADB，求∠ADB的度数．