「初中数学」三角形三边关系的六种应用

三角形的三边关系为:三角形，任意两边的和大于第三边，任意两边的差小于第三边.由于是线段的不等量关系，我们在遇到求边或周长的范围以及一些不等量的习题时，就要想到利用这一性质，常见的应用如下:

一.判断三条线段能否组成三角形(最直接的方法是，若两条短线段的和大于最长的线段，则此三线段可构成三角形)

1.下列各组数中，不可能成为一个三角形三边长的是(____)

A.2，3，4.B.5，6，7.C.5，6，12.D.6，8，10.

2.下列长度的三条线段不能组成三角形的是(____)

A.5，5，10.B.4，5，6.C.4，4，4.D.3，4，5.

二.求三角形第三边的长或取值范围

3.若a，b，c为三角形的三边长，且a，b满足|a²一9|+(b一2)²=0，则第三边长a的取值范围是______.

4.若一个三角形的两边长分别为5和8，则第三边长可能是(______).

A.14.B.10.C.3.D.2.

5.若三角形的两边长分别为3和5，则周长L的取值范围是(_____).

A.6<L<15.B.6<L<16.C.11<L<13.D.10<L<16

6.一个三角形的两边长分别为5㎝和3㎝，第三边的长是整数，且周长是偶数，则第三边的长是(_____).

A.2㎝或4㎝.B4㎝或6㎝.C.4㎝.D.2㎝或6㎝.

三.求等腰三角形的边长及周长

7.已知实数x，y满足|x一4|+(y一8)²=0，则以x，y的值为两边长的等腰三角形的周长是(____).

A.20或16.B.20.C.16.D.以上均不对.

8.若等腰三角形的周长为10㎝，其中一边长为2㎝，则该等腰三角形的底边长为(_)

A.2㎝，B.4㎝.，C.6㎝，D.8㎝.

9.已知在△ABC中，AB=5，BC=2，且AC的长为奇数.

(1)求△ABC的周长;

(2)判断△ABC的形状.

解:(1)∵AB=5，BC=2，∴3<AC<7，又∵AC的长为奇数，∴AC=5，∴△ABC的周长为5+5+2=12.

(2)∵AB=AC=5，∴△ABC是等腰三角形

四.化简含绝对值的式子

10.已知a，b，c为三角形的三边长，化简:|b+c一a|+|b一c一a|一|c一a一b|一|a一b+c|.

【分析】化简绝对值，关键判断绝对值里边的代数式是正数、负数还是零.是正数或零，去掉绝对值，代数式保持不变;是负数，去掉绝对值后，代数式变为原来的相反数，之后，能合并的再合并同类项.本题通过三角形三边关系判断绝对值里边代数式的正、负情况.

解:∵a，b，c为三角形的三边长，∴b+c>a，a+c>b，a+b>c，∴b+c一a>0，b一c一a<0，c一a一b<0，a一b+c>0，∴原式=(b+c一a)一(b一c一a)+(c一a一b)一(a一b+c)=2c一2a.

五.证明线段不等关系

10.如图，已知P是△ABC内一点，求证:PA+PB+PC>(AB+BC+AC)

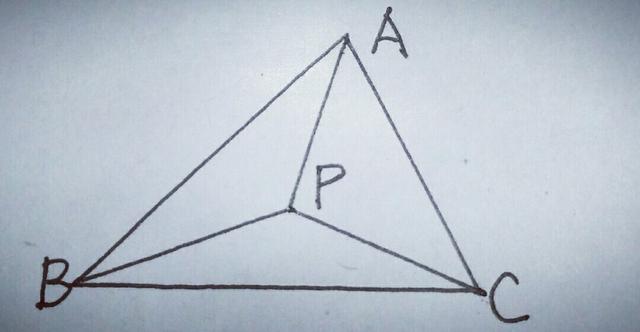
【分析】AP，BP，CP把△ABC分为三个三角形，每个三角形两边和大于第三边，AP，BP，CP正好各用两次，也即2PA+2PB+2PC>AB+BC+AC，也即得证.

证明:在△ABP中，PA+PB>AB，在△ACP中，PA+PC>AC，在△BPC中，PB+PC>BC，∴2(PA+PB+PC)>AB+BC+AC，即PA+PB+PC>(AB+BC+AC)/2.

11.如图，P是正方形ABCD的边DC延长线上的一点，连结PA交BC于点E，求证:AP>AC.

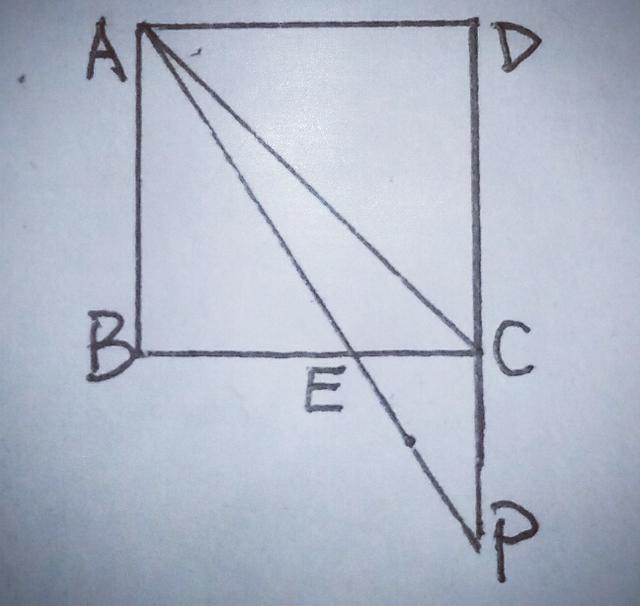
【分析】证明线段不等关系，想到三角形三边关系，可AC，AP，PC是在一个三角形中，但又引进了PC，那么就想到把AP折成两条线段和AC围成一个三角形，那么又怎样把AP分成两段呢？从图看∠ECP=90°，想到直角三角形斜边的中线，如图

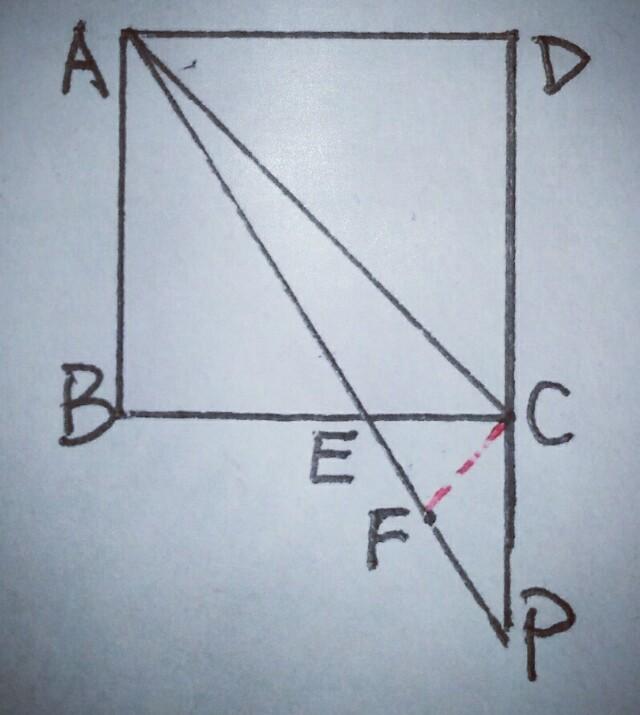
取PE的中点F，连结CF，则PF=CF，这样成功的把AP段分成AF，PF两段，CF等量代换PF，在△ACF中利用三边关系可证.

证明:取PE的中点F，连接CF，∵四边形ABCD是正方形，∴BC⊥DP，∴CF=FP=PE/2，在△AFC中，有AF十FC>AC，∴AF十FP>AC，即AP>AC.

12.如图，已知:D是△ABC的外角∠EAC的平分线上的一点.求证:DB+DC>AB+AC.

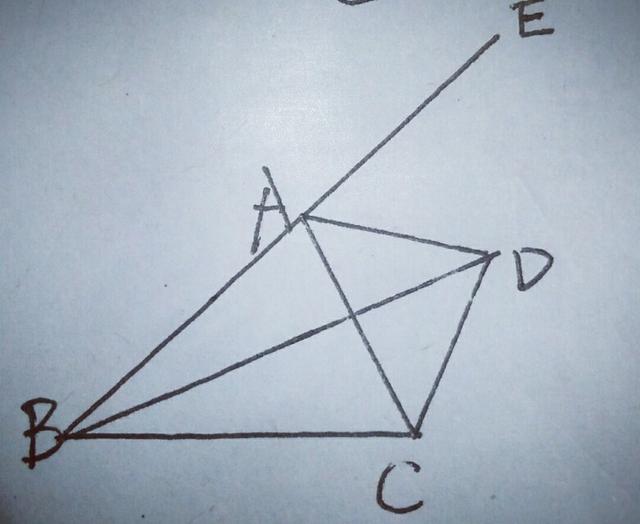
【分析】要证DB+DC>AB+AC，可用三角形三边关系定理，但必须把BD、DC、AB+AC移到一个三角形中，可以从构造AB+AC入手，由于AD平分∠EAC，利用角平分线的对称性，将AC，AB移在一条线上，同时能将CD边进行转换，如图，

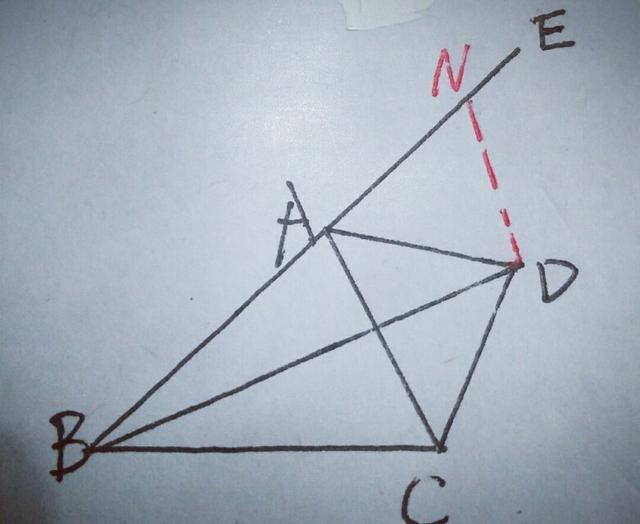
在BA的延长线AE上截取AN=AC，连接DN则可构造出△DAN≌△DCA，则AC=AN，DC=DN，达到了所要的目的在△BDN中，BD+DN(DC)>AN(AB+AC).

证明:在BA的延长线AE上截取AN=AC，连接DN，∵AD平分∠EAC，∴∠EAD=∠CAD，AD=AD，AN=AC，∴△ADN≌△ADC，∴DN=DC，在△BDN中，BD+DN>BN，∴BD+DC>AB+AC.

13.如图，P为△ABC内一点，求证:AB+AC>PB+PC.

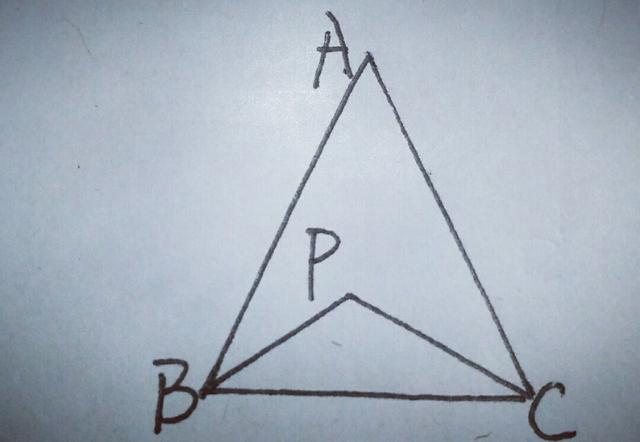
【分析】直接运用图中的△ABC和△PBC得到的AB+AC>BC，PB+PC>BC，不能解决问题，为使PB和CP同时出现在大于号右侧，则应构造新的三角形，可延长BP交AC于点D，或过点P作一直线.

证明:(一)如图，延长BP交AC于点D，

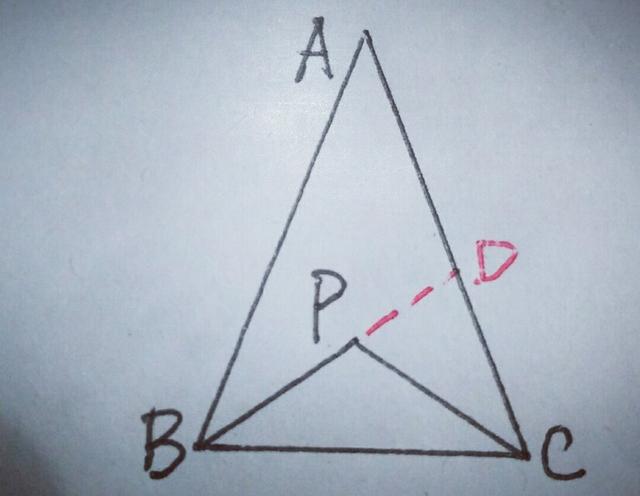
在△ABD中，AB+AD>BD，即AB+AD>BP+PD，在△CDP中CD+PD>PC，∴AB+AD+CD+PD>BP+PD+PC，∴AB+AD+CD>BP+PC，即AB+AC>BP+PC.

证明:(二)如图，过点P任作一直线交AB于E交AC于F

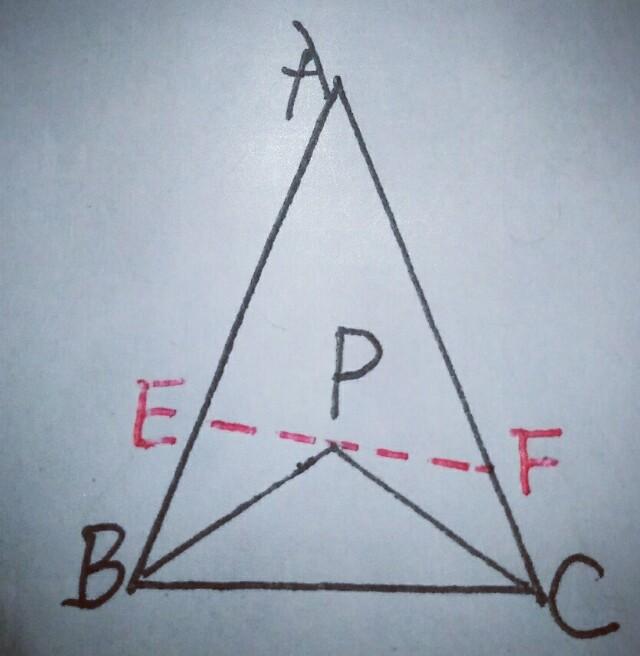
在△AEF中，AE+AF>EP+PF，在△BEP中，BE+EP>PB，在△PFC中，FC+PF>PC，∴(AE+BE)十(AF+FC)十EP+PF>PB+PC+EP+PF，∴AB+AC>PB+PC.

六.利用三角形三边关系求最值

13.如图∠MON=90°，矩形ABCD的顶点A，B分别在OM，ON上，当点B在边ON上运动时，点A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，在运动过程中，点D到点O的最大距离是多少？

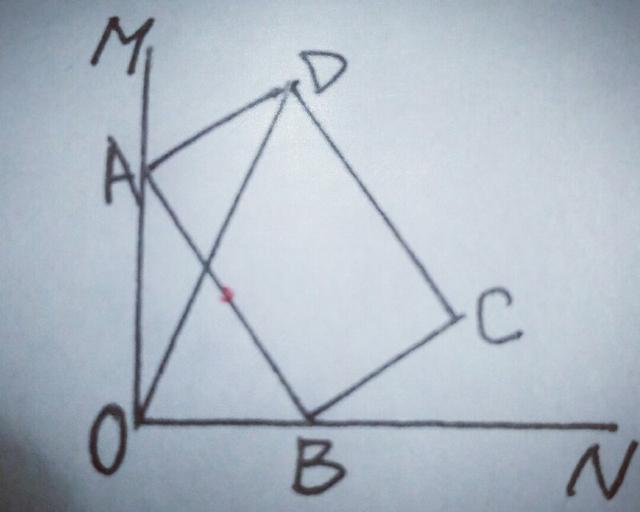
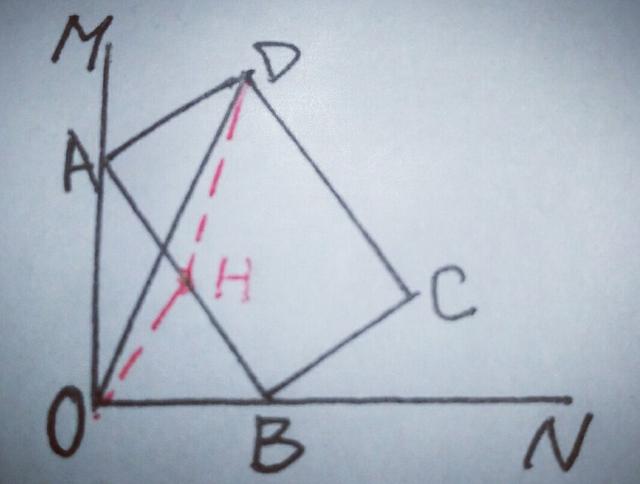
【分析】动点问题，总的方法是，以静制动，取AB的中点H，OH=AB/2不变，由勾股定理得AD²+AH²=DH²，∴DH=√2，也不变，在△DOH中，OH在变，有OH+DH≥DO，则点D、H、O三点共线时取等号，所以点D到点O的最大距离为OH+DH=√2+1，如图.

前八题答案如下:

1.C，2.A，3.1<c<5，4.B，5.D，6.B，7.B，8.A.