反比例函数是初三下学期的内容，自然也是近年来中考的热点。综合题大致有以下类型:

一：反比例函数与一次函数综合

主要考点:反比例函数的基本定义及性质；一次函数的基本定义及性质。

二：反比例函数与二次函数的综合

主要考点:反比例函数的基本定义及性质；二次函数的基本定义及性质。

三：反比例函数与几何图形的综合问题

主要考点:反比例函数的基本定义及性质；反比例函数图像上点的坐标特征；几何图形的基本知识。

真题求解

如图①，已知双曲线y=1/x(x>0)，直线L1:y-√2=k(x-√2)(k<0)过定点F且与双曲线交于A，B两点，设A(x1，y1)，B(x2，y2)(x1<x2)，直线L2:y=-x+√2.

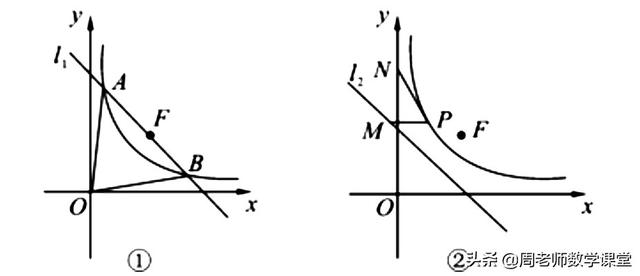
⑴ 若k=-1，求△OAB的面积S；

⑵ 若AB=5/2√2，求k的值；

⑶ 如图②，设N(0，2√2)，P在双曲线上，M在直线L2上且PM∥x轴，求PM+PN最小值，并求PM+PN取得最小值时P的坐标。[参考公式：在平面直角坐标系中，若A(x1，y1)，B(x2，y2)，则A，B两点间的距离为：AB=√(ⅹ1-x2)*2+(y1-y2)*2]

解题方法提示

分析题意，对于⑴，要求S△OAB，设直线L1与y轴交于点C，则可将△OAB的面积看作是以OC为底，B的横坐标为高的三角形面积与以OC为底，以A的横坐标为高的三角形面积之差；

根据上述提示可知，需要计算出A、B两点的横坐标，将k=-1代入L1，联立直线方程和双曲线方程即可求出两点横坐标，从而解答⑴；

对于⑵，已知A、B为直线L1与双曲线的交点，先联立直线方程和双曲线方程，判断△是否大于等于0，然后结合根与系数的关系与两点间的距离公式进行解答；

对于⑶，已知点P在双曲线上，可设出点P的坐标，根据PM∥x轴可知M点与P点的纵坐标相同，结合M点在直线L2上可得点M的坐标；

根据两点间的距离公式可知PM=PF，在△PNF中根据三角形的三边关系进行解答即可，求出等号成立时P点的坐标即可求出PM+PN的最小值。

解题步骤

解:⑴当k=-1时，L1为y=-x+2√2，联立得，

y=-x+2√2，y=1/x

化简得x*2-2V√2x+1=0，

解得：x1=√2-1，x2=√2+1.

设直线L1与y轴交于点C，则C(0，2√2)

S△OAB=S△BOC-S△AOC=1/2·2√2·(ⅹ2-x1)

⑵ 根据题意得：

y-√2=k(x-√2)，y=1/x

整理，得

y=kx*2+√2(1-k)x-1=0(k>0).

∵△=[√2(1-k)]*2-4xkx(-1)=2(1+k*2)>0，

∴该方程有两个不相等的实数根，

∴Ⅹ1、X2是方程的两根，

∴X1+X2=√2(K-1)/k，X1·X2=-1/k

∴AB=√(X1-X2)*2+(y1-y2)*2

= √(X1-X2)*2+(1/X1-1/Ⅹ2)*2

= √(X1-X2)*2+(X1-Ⅹ2/X1·X2)*2

=√(X1-Ⅹ2)*2·(1+1/X1*2·Ⅹ2*2)

=√[(Ⅹ1+X2)*2-4X1·X2](1+1/X1*2·X2*2)

∴AB=√2(k*2+1)*2/k*2=√2(k*2+1)/-k(k＜0)，

∴√2(K*2+1)/-k=5√2/2，整理得:

2K*2+5K+2=0，解得:k=-2或k=-1/2.

⑶ F(√2，√2)，连接PF，如图，

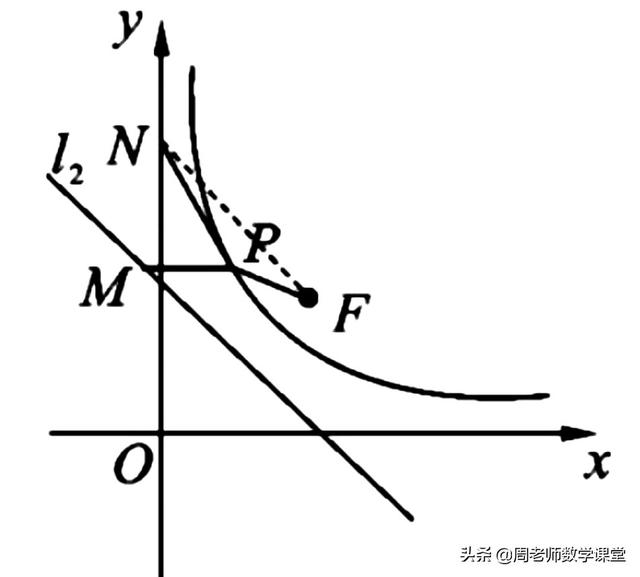
设P(x，1/ⅹ)，则M(-1/ⅹ+√2，1/ⅹ)，

则PM=x+1/ⅹ-√2=√(ⅹ+1/ⅹ-√2)*2

=√x*2+1/ⅹ*2-2√2(ⅹ+1/ⅹ)+4.

∵PF=√(x-√2)*2+(1/x-√2)*2，

=√x*2+1/x*2-2√2(x+1/x)+4

∴PM=PF.

∴PM+PN=PF+PN≥NF=2.

当点P在NF上时等号成立，此时NF的解析式为y=-x+2√2.

由⑴知P(√2-1，√2+1)，

∴当P(√2-1，√2+1)时，PM+PN的最小值是2.

解题总结

上述真题是反比例函数、一次函数和几何图形的综合题，难度系数还是蛮大，基础不扎实的同学，可以说几乎没有思路，根据题意，对函数的定义及性质，反比例函数图像上点的坐标特征都要熟悉，三角形的知识也要了如之掌，再结合题目中的参考公式，应该有思路吧，当然一元二次方程中韦达定理的灵活运用，三角形三边关系的应用也是解题的关键。