一、选择题(本题10个，每小题3分，共30分)

1.下列图形既是轴对称图形，又是中心对称图形的是( )

A.等边三角形

B.平行四边形

C.正五边形

D.正方形

2.若△ABC相似△A'B'C’，面积比为1：2，则△ABC与△A'B'C'的相似比为( )

A.1:√2

B.1:4

C.4:1

D.√2:1

3.“抛一枚均匀硬币，落地后正面朝上“这一事件是( )

A.必然事件

B.随机事件

C.确定事件

D.不可能事件

4.如果一个扇形的半径是1，弧长是π/3，那么此扇形的圆心角的大小为( )

A.30°

B.45°

C.60°

D.90°

5.一元二次方程x*2-2x=m总有实数根，则m应满足的条件是( )

A.m>-1

B.m=-1

C.m≥-1

D.m≤1

6.二次函数y=ax*2+bx+c的图象如图所示，则下列结论中正确的是( )

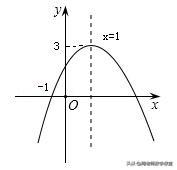
A.a>0

B.关于x的一元二次方程ax*2+bx+c=3有两个相等的实数根

C.c<0

D.当x≥1时，y随x的增大而减小

7.一个可以改变体积的密闭容器内装有一定质量的某种气体，当改变容器体积时，气体的密度也随之改变。密度ρ(单位：kg/m*3)与体积V(单位：m*3)满足函数关系式ρ=k/V(k为常数，k≠0)，其图象如图所示，那么当V≥6m*3时，气体的密度ρ(单位:kg/m*3)的取值范围是( )

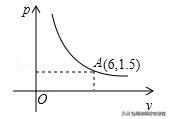
A.ρ≤1.5kg/m*3

B.0kg/m*3<ρ<l.5kg/m*3

C.ρ≥1.5kg/m*3

D.ρ>1.5kg/m*3

8.要组织一次篮球邀请赛，参赛的每两个队都要比赛一场，根据场地和时间等条件，计划共安排28场比赛，设比赛组织共邀请x对参加比赛，则依题意可列方程为( )

A.1/2ⅹ(x-1)=28

B.1/2x(x+1)=28

C.ⅹ(ⅹ-1)=28

D.ⅹ(ⅹ+1)=28

9.如图，⊙O是△ABC的外接圆，∠B=60°，AC=8，则⊙O的直径AD的长度为( )

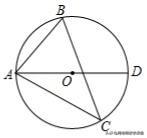
A.16

B.4

C.8√3/3

D.16√3/3

10.如图，点P(ⅹ，y)(x>0)是反比例函数y=k/ⅹ(k>0)的图象上的一个动点，以点P为圆心，OP为半径的圆与x轴的正半轴交于点A.若△OPA的面积为S，则当x增大时，S的变化情况是( )

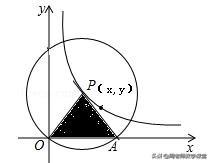
A.S的值增大

B.S的值减小

C.S的值先增大，后减小

D.S的值不变

二、填空题(每小题3分，共18分)

11.请写一个图象在第二、四象限的反比例函数解析式:______。

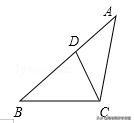
12.如图，在△ABC中，AB=8，AC=6，D是AB边上的一点，当AD=______时△ABC∽△ACD.

13.已知x=-2是方程x*2-mx-6=0的一个根，则方程的另一个根是______。

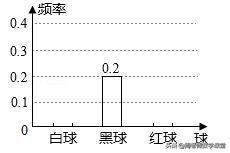
14.一个布袋中装有只有颜色不同的a(a>12)个小球，分别是2个白球、4个黑球，6个红球和b个黄球，从中任意摸出一个球，记下颜色后放回，经过多次重复实验，把摸出白球，黑球，红球的概率绘制成统计图(未绘制完整）.根据题中给出的信息，布袋中黄球的个数为_____。

15.把抛物线y=-2x*2先向左平移1个单位，再向下平移2个单位长度后，所得函数的表达式为_________。

16.如图，半圆O的直径AB长度为6，半径OC丄AB，沿OC将半圆剪开得到两个圆心角为90°的扇形.将右侧扇形向左平移，使得点A与点O’，点O与点B分别重合，则所得图形中重盖部分的面积为_______。

三、解答题(共72题)

17.解下列方程

⑴ x*2+10x=3

⑵ 6+3x=x(x+2)

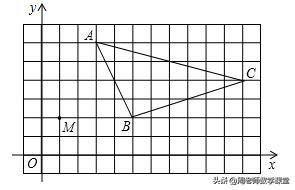
18.在如图所示网格图中，已知△ABC和点M(1，2)

⑴ 在网格中以点M为位似中心，画△A’B'C'，使其与△ABC的位似比为1：2.

⑵ 写出△A'B'C'的各顶点坐标.

19.如图，一次函故y=-x+b分别与x轴、y轴交于A、B两点，与反比例函数y=k/ⅹ(k≠0)交于点C，A点坐标为(2，0)，B点是线段AC的中点.

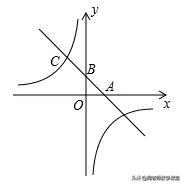
⑴ 求一次函数与反比例函数的解析式

⑵ 根据图象写出，在第二象限内，一次函数的值小于反比例函数的值的x的取值范围，

20.双十一期间，某商厦为了促销，将两张形状完全相同的图片(如图1)从中间剪开，再把得到的四张形状相同的小图片混合在一起(如图2)，放到一个暗箱中，如果顾客在该商厦一次购物满300元，就可以获得一次抽奖机会，其规则是：从四张图片中随机摸取一张，接着再随机摸取一张，如果抽出的两张小图片恰好能合成一张完整的图片，则可以返还20元的购物券，问：一次抽奖，顾客获得购物券的概率是多少?

21.某商场经营某种电子产品，平均母天可销售30件，每件盈利50元为了实现每天的平均利润曾长40%的目标，该商场的市场都经过调查得知，若每件商品每降价1元，商场平均每天可多售出2件该电子产品.问：每件商品降价多少元时，商场可以实现所提出的润增长目标?

22.(10分)如图，在△ABC中，AB=AC，以AB为直径作⊙O交BC于点D，交AC于点G，过点D作DE丄AC于点G，延长ED交AB的延长线于点F.

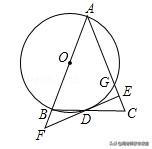
⑴ 判断直线EF与O0的位置关系，并说明理由.

⑵ 若AB=13，BC=10.求AE的长.

23.(12分)【实验观察】

⑴ 观察下列两个数的乘积(两个乘数的和为10)，猜想其中哪两个数的乘积最大(只写出结论即可)，1x9，2x8，3x7，.…8x2,9x1

⑵ 观察下列两个数的乘积(两个乘数的和为100)，猜想其中哪两个数的乘积最大(只写出结论即可).45x55，46x54，47x53，54x46，55x45.

【精想验证】根据上面活动给你的启示，猜想，如果两个正乘数的和为m(m>0)，你认为

两个乘数分别为多少时，两个乘数的乘积最大?用所学知识说明你的猜想的正确性。

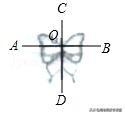
【拓展应用】小明欲制作一个四边形的风筝(如图所示)，他想用长度为1.8m的竹签制作风筝的骨架AB与CD(AB丄CD)，为了使风筝在空中能获得更大的浮力，他想把风筝的表面积(四边形ADBC的面积)制作到最大.根据上面的结论，求当风筝的骨架AB、CD的长为多少时，风筝的表面积能达到最大?

24.(12分)旋转变换在平面几何中有着广泛的应用.特别是在解(证)有关等腰三角形、正三角形、正方形等问题时，更是经常用到的思维方法，请你用旋转交换等知识，解决下面的问题，如图1，△ABC与△DCE均为等腰直角三角形，DC与AB交于点M，CE与AB交于点N

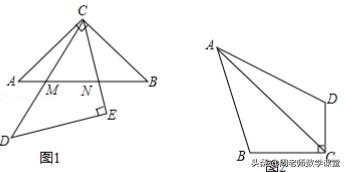
⑴ 以点C为中心，将△ACM逆时针旋转90°，画出旋转后的△A'CM’

⑵ 在⑴的基础上，证明AM*2+BN*2=MN*2.

⑶ 如图2，在四边形ABCD中，∠BAD=45°，∠BCD=90°，AC平分∠BCD，若BC=4CD=3，则对角线AC的长度为多少？(直接写出结果即可，但在图中保留解决问题的过程中所作辅助线、标记的有关计算数据等)。