反比例函数临界点问题

我们有时会遇到这一类问题，反比例函数与某一区域边界有交点，求k的取值范围，解决这类问题，一定要结合反比例函数图像，仔细分析，有时候问题可能并没有你想的那么简单，本节我们来一起学习一下这类问题的处理办法。

首先我们来看几个基本问题：

1、如图，在平面直角坐标系中，A(2，1)，B(1，3)，C(3，2)，若函数y=k/x（x＞0）的图象与△ABC的边有公共点，求k的取值范围。

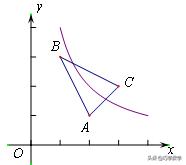
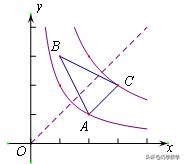
要使函数y=k/x（x＞0）的图象与△ABC的边有公共点，只需考虑两个临界位置，

结合反比例函数图像的对称性，它是关于直线y=x对称的，

可知过点A（2，1）时，是k最小的位置；过点C（3，2）时，是k最小的位置.

∴2×1≤ k≤ 3×2，即2≤ k ≤6．

2、若将上题中的C点坐标改为（1，3），那么临界位置会发生改变吗？k的取值范围又是多少呢？

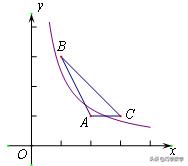
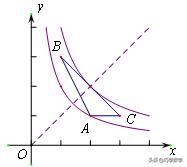
由图像可知，此时使得k最小的临界位置依然是A点，但是k最大的临界位置不在C点了，由于B、C两点关于直线y=x对称，因此当函数y=k/x（x＞0）的图象与线段BC刚好只有一个交点时，k是最大的，此时图像过BC的中点（2，2），k=4，因此2≤ k ≤4.

从以上两个基本问题，我们可以看出，处理临界问题的时候，一定要结合图像对称性以及区域的特点，仔细分析计算，才能确保万无一失。

当然，y=x这条直线对我们的分析是非常有帮助的，同学们在下面的例题及练习中不妨试着去操作一下吧。

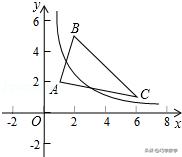
例1：如图，△ABC的三个顶点分别为A（1，2），B（2，5），C（6，1）．若函数y=k/x在第一象限内的图象与△ABC有交点，则k的取值范围是　 　．

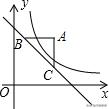
例2：如图，过点A（4，5）分别作x轴、y轴的平行线，交直线y=﹣x+6于B、C两点，若函数y=k/x（x＞0）的图象与△ABC的边有公共点，则k的取值范围是（ ）

A．5≤ k≤20 B．8≤ k≤20 C．5≤ k≤8 D．9≤ k≤20