「初中数学」利用勾股定理解题的几种常见题型（上）

一.利用勾股定理求线段长

1.如图，在等腰直角三角形ABC中，∠ABC=90°，点D为AC边的中点，过D点作DE⊥DF，交AB于E，交BC于F，若AE=4，FC=3，求EF的长.

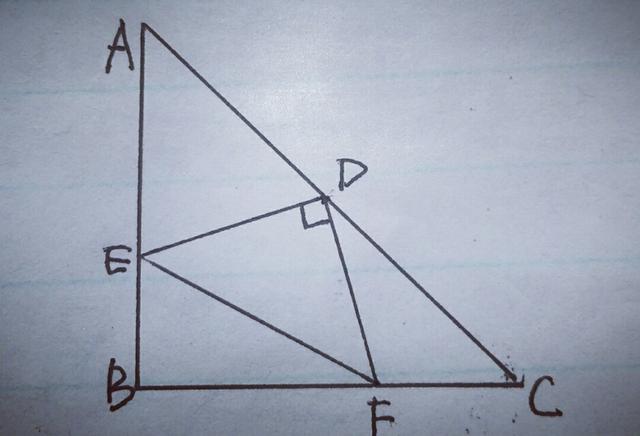
【分析】由于D是等腰三角形ABC斜边AC的中点，想到"三线合一"所以连接BD，如图

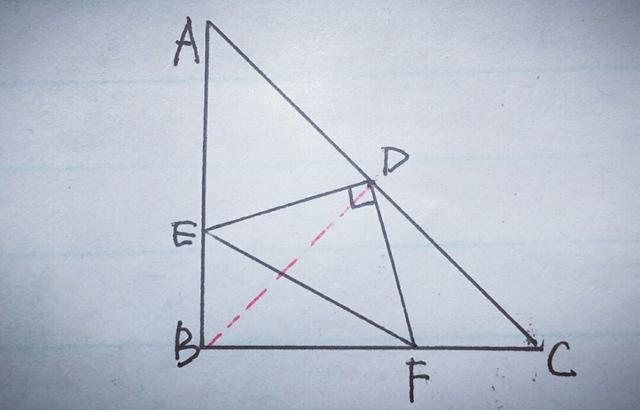
则BD⊥AC，∠ADB=∠CDB=90°，AD=BD，又DE⊥DF，∴∠EDF=90°，∴∠ADE=∠BDF，易知∠A=∠DBF=45°，∴△ADE≌△BDF，∴AE=BF=4，而FC=3，∴AB=BC=7，∴BE=3，在Rt△EBF中，由勾股定理得EF²=BE²+BF²，∴EF=5.

2.如图，一只蚂蚁若沿长方体表面从A点爬到B'点所行路程最短为多少？(AC=2㎝，AA'=4cm，BC=1㎝).

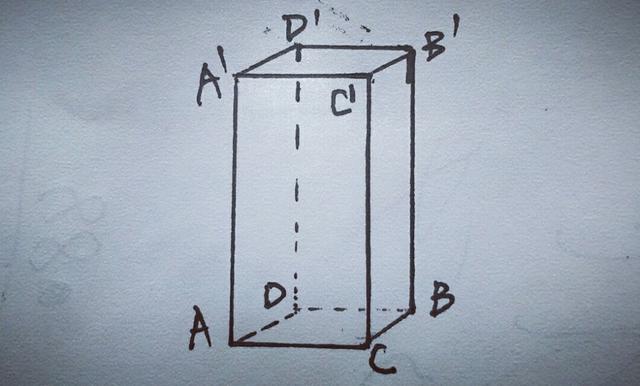
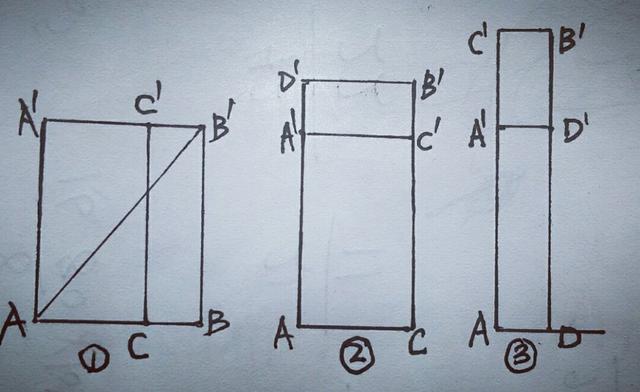
【分析】本题运用转化的思想，是最短行程问题，从A点到B'点有三种走法，依据两点间线段最短，根据勾股定理求出最短路程.①如图①，沿AC，BC，AA'，A'C'，B'B，C'B'剪开展为一个平面图形，在AA'B'这一直角三角形中，求得AB'²=25㎝;②如图②，沿AC，CC'，C'B'，D'A'，AA'，B'D'剪开展为一个平面图形，在AD'B'这一直角三角形中，求得AB'²=29;③如图③，沿AD，DD'，B'D'，C'B'，C'A'，AA'剪开展为一个平面图形，在AC'B'这一直角三角形中，求得AB'²=37，分析比较得AB'最短为5㎝.

3.如图，折叠长方形一边AD，使点D落在BC上点F处，AB=8㎝，BC=10㎝，求EC的长.

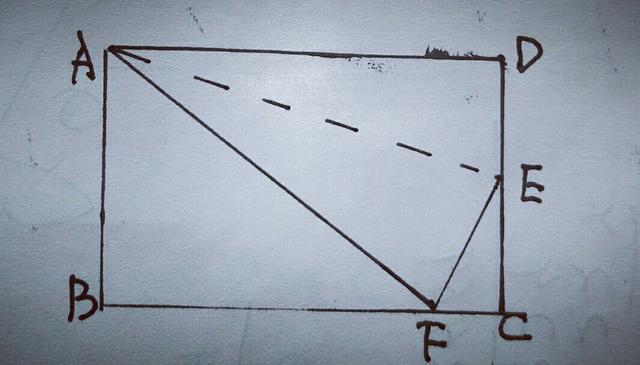
【分析】本题属折叠问题，方法是设出未知数，表示相关的量，进而利用勾股定理列方程求解.设EC为x㎝，则DE=8一x=EF，而由折叠知AF=AD=10，∴在Rt△ABF中，由勾股定理求得BF=6㎝，∴CF=4㎝，在Rt△ECF中，EC²+CF²=EF²，即x²+4²=(8一x)²，解得x=3，∴EC长为3㎝.

4.如图，在△ABC中，∠ACB=90°，CD⊥AB于D，点B关于CD的对称点为B'且GB'⊥B'C，交AC于G，若AB=5，BC=3，求AG的长.

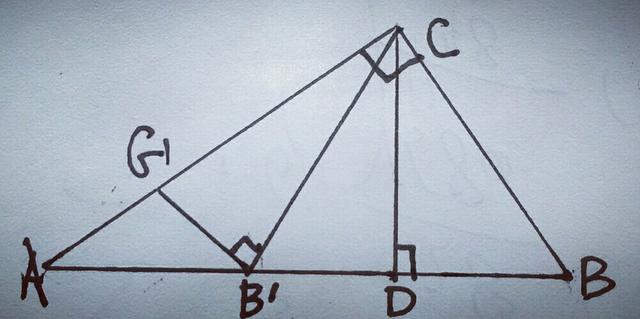
【分析】在Rt△ACB中，AB=5，BC=3，由勾股定理得，AC=4，又CD⊥AB，点B关于CD的对称点为B'，∴B'C=BC=3，∠B=∠CB'B，而∠A+∠B=90°，∠GB'A+∠CB'B=90°，∴∠A=∠GB/A，∴AG=B'G，设AG=x，则CG=4一x，在Rt△GB'C中，GB'²+B'C²=CG²，即x²+3²=(4一x)²，解得x=7/8，即AG长为7/8.

二.利用勾股定理证明线段之间的平方关系

5.如图，∠C=90°，AM=CM，MP⊥AB于点P，求证:BP²=BC²+AP².

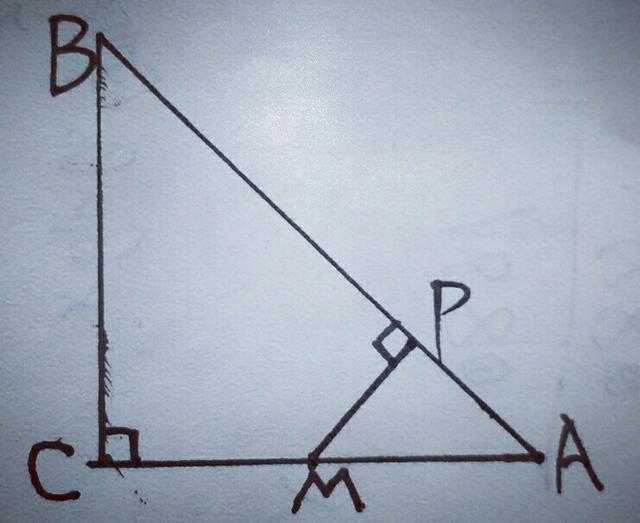
【分析】此类题一般都是利用勾股定理，结合图形的特点进行推导，几何题用代数法进行证明，体现了数与形的完美结合，本题BP边必须处在一个直角三角形中，所以连接BM，如图

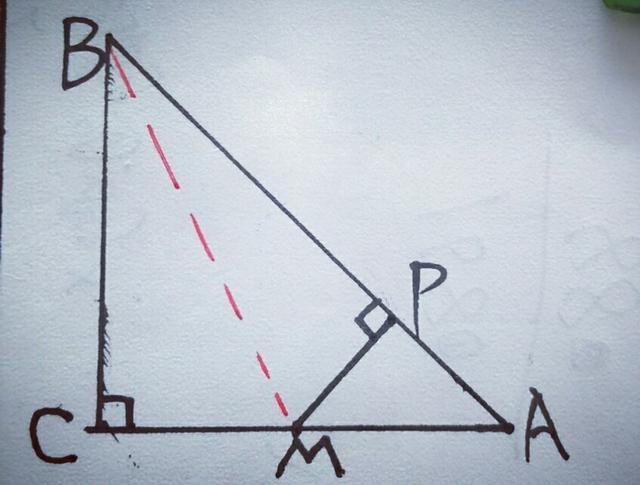
则在Rt△BPM中，BP²=BM²一MP²，而在Rt△BCM中BM²=BC²+CM²，∴BP²=BC²+CM²一MP²，而AM=CM，∴BP²=BC²+AM²一MP²，在Rt△APM中，AM²一MP²=AP²，∴BP²=BC²+AP².

6.如图，在△ABC中，AB=AC，P是BC边上任意一点，连接AP，求证:AC²=AP²+CP×BP.

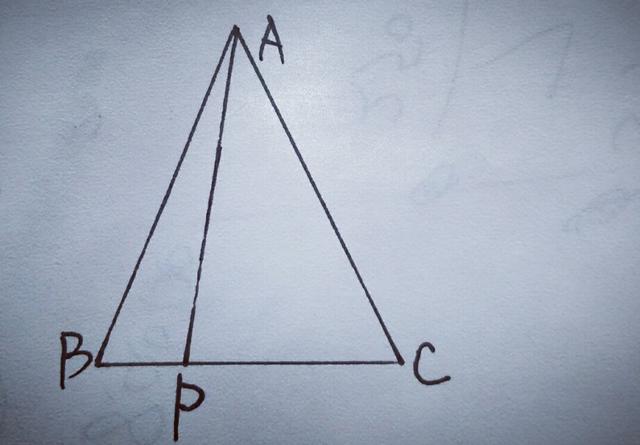
【分析】要证线段间的平方关系，应用勾股定理，应构建直角三角形，所以过点A作AD⊥BC于D，D为垂足，如图

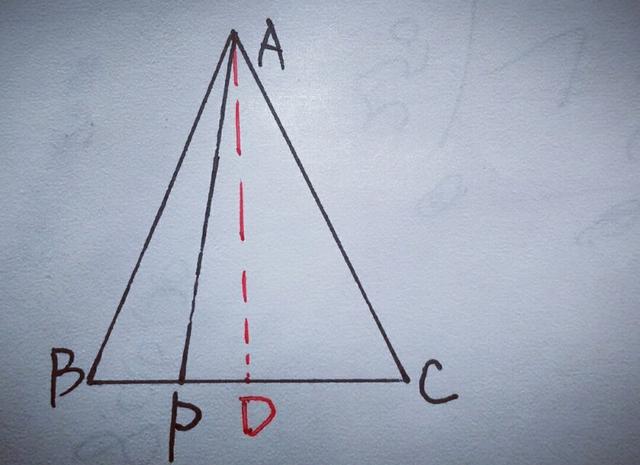
由于AB=AC，∴BD=DC，在Rt△AD中，AC²=AD²+DC²，在Rt△APD中，AD²=AP²一PD²，∴AC²=AP²一PD²+DC²=AP²+(DC+PD)(DC一PD)=AP²+CP(DC一PD)，而DC=BD，∴AC²=AP²+CP×BP.

7.如图，在△ABC中，AB=AC，∠BAC=90°，D是BC上任意一点，求证:BD²+CD²=2AD².

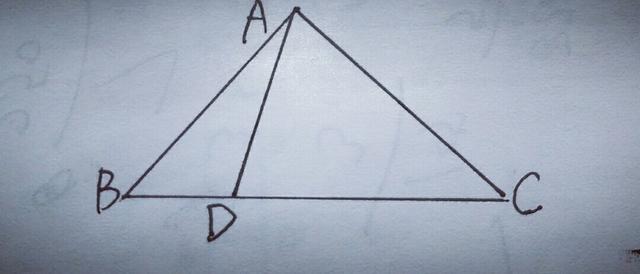
【分析】由题知△ABC为等腰直角三角形，想到三线合一出直角，所以过A点作AE⊥BC于E，E为垂足，如图

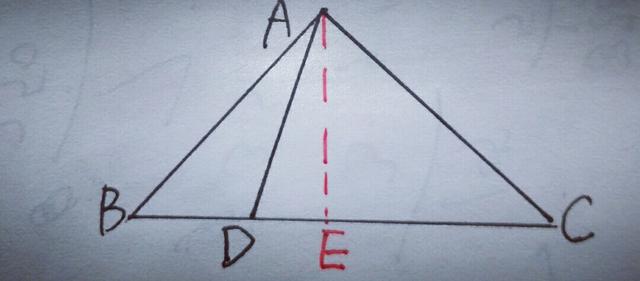
则AE=BE=CE，证题时步步向结论靠近，∵BD²=(BE一DE)²=(AE一DE)²=AE²一2AE×DE+DE²，CD²=(CE+DE)²=(AE十DE)²=AE²+2AE×DE十DE²，∴BD²+CD²=2AE²十2DE²=2AD².这里巧用完全平方公式进行了转换.

8.如图，在△ABC中，∠ACB=90°，CD⊥AB于D，设AC=b，BC=a，AB=c，CD=h，求证:①1/a²+1/b²=1/h²，②a+b<c+h，③以a+b，h，c+h为边长的三角形是直角三角形.

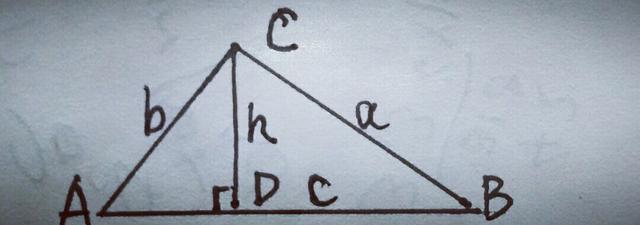
【分析】①左边通过运算，结合勾股定理，结论中有了高h，则要用到面积公式，∴1/a²十1/b²=(a²+b²)/a²b²=c²/a²b²，而ab/2=ch/2，∴a²b²=c²h²，∴1/a²+1/b²=1/h².

②是比较大小，需运用勾股定理结合完全平方公式进行推证，∵(a十b)²=a²十b²+2ab=c²+2ab，又ab=ch，∴(a+b)²=c²+2ch<c²+2ch+h²=(c十h)²，∴a十b<c十h.

③由上知c十h最大，∵(a十b)²=a²十b²+2ab，∴(a+b)²+h²=a²+b²+2ab十h²=c²+2ch+h²=(c+h)²，∴以a+b，h，c+h为边长的三角形是直角三角形.