二次函数压轴题18，与几何图形的综合探究

【题目呈现】

【思路分析】

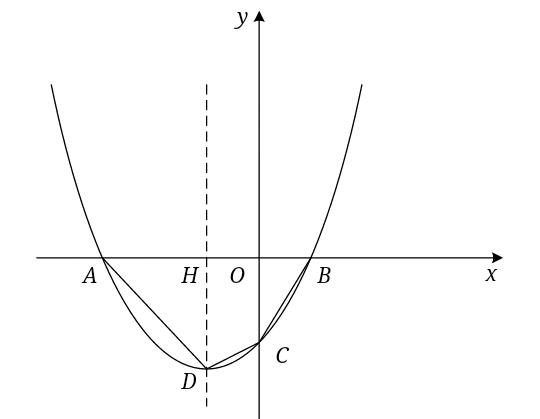
(1)将C点坐标代入抛物线解析式即可求得a的值，再令y=0，即可求解A、B两点坐标。

(2)先通过抛物线解析式求得D点坐标，根据A、B、C、D四点生标可得各相关线段的长度，从而算得四边形ABCD的面积，再分情况讨论直线L在不同侧所截三角形面积为3时的两种情况，分別在确定三角形顶点坐标后使用待定系数法求解直线L的解析式。

(3)先分别设直线PQ、DN的解析式，再根据解析式联立方程组得到点M、N的坐标，然后通过菱形四边相等的性质与两点间距离公式建立方程求解，最后检验结果是否正确即可。

【答案与解析】

解:(1)将C点坐标(0，8)代入抛物线解析式得，一8/3=a(0+1)²一3，解得a=1/3，∴抛物线解析式为y=1/3(x十1)²一3，令y=0，得0=1/3(x十1)²一3，解得x=2或一4，∴A点坐标为(一4，0)，B点坐标为(2，0).

(2)∵抛物线解析式为y=1/3(x+1)²一3，∴顶点D的坐标为(一1，一3)，又∵A(一4，0)，B(2，0)，C(0，一8/3)，∴AH=HD=3，OH=1，OC=8/3，BO=2，∴S四边形ABCD=S△AHD十S梯形CDHO+S△BOC=1/2×AH×HD十1/2(HD+OC)×OH+1/2×BO×OC=10，当直线L将四边形ABCD面积分为3:7两部分时，因S△AHD=9/2>3，S△HBC=1/2×HB×CD=4>3，所以只有直线L交AD或BC时才符合题意。

如图1，

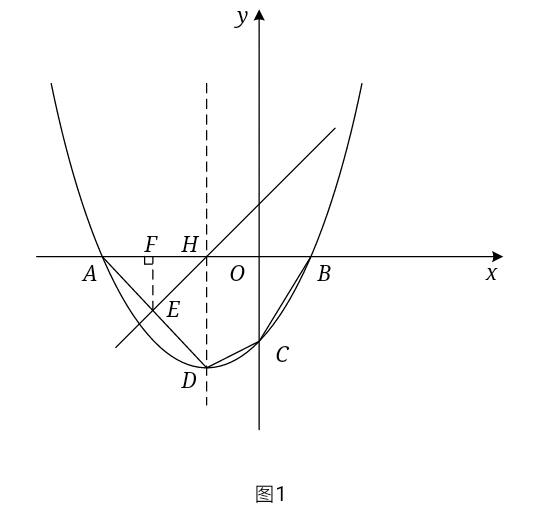
当直线L交直线AD于E且符合题意时，过E作EF⊥x轴于F，则S△AEH=1/2×AH×EF=3，则EF=2，∴E点纵坐标为一2，设直线AD的解析式为y=K1x+b1，将A(一4，0)，D(一1，一3)两点代入得，

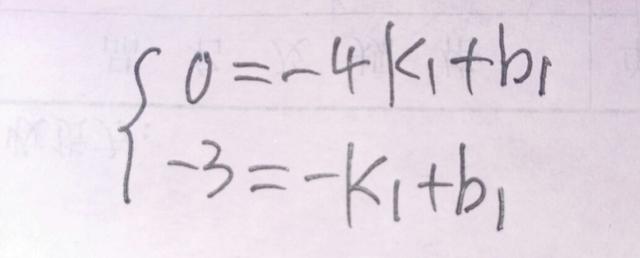
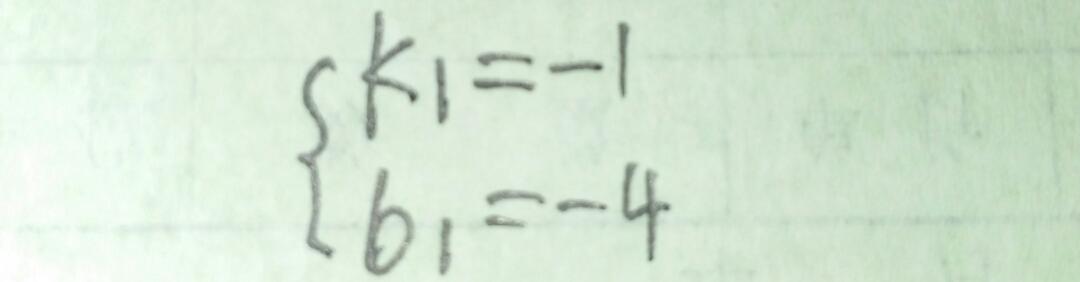
故直线AD的解析式为y=一x一4，令y=一2，得x=一2，故E点坐标为(一2，一2)，设直线EH的解析式为y=K2x十b2，将E(一2，一2)，H(一1，0)两点坐标代入得

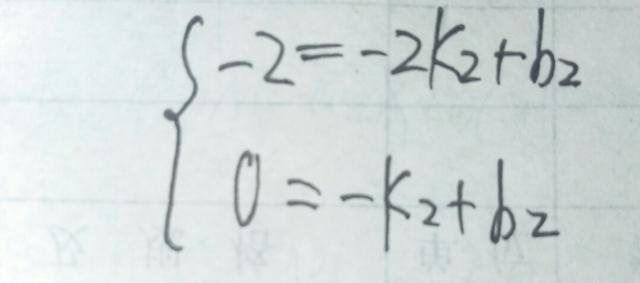
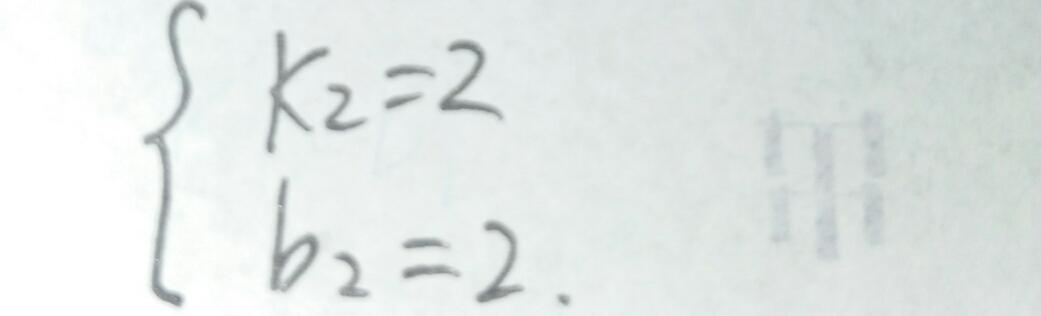
故直线EH的解析式为y=2x+2.

如图2

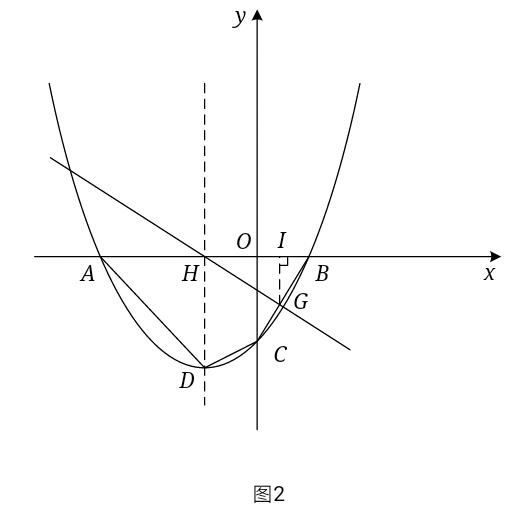
当直线L交直线BC于G且符合题意时，过G作GI⊥x轴于I，同上可得G点纵坐标为一2，又直线BC的解析式为y=4x/3一8，令y=一2，得x=1/2，故G点坐标为(1/2，一2)，同上可得直线HG的解析式为y=一4x/3一4/3，∴直线L的表达式为y=2x十2或y=一4x/3一4/3.

(3)如图3，

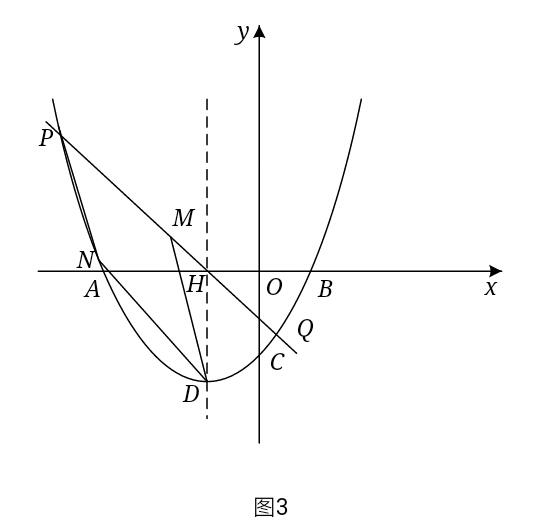
在第二象限的抛物线上取一点P，连接PH交抛物线于另一点Q，取PQ的中点为M，过点D作DN∥PQ交抛物线于N，连接PM、PN、DM、DN，设直线PQ的解析式为y=K3x+b3，将H(一1，0)代入得0=一K3+b3，得b3=K3，故直线PQ的解析式为y=K3x+K3，将它与抛物线的解析式联立得

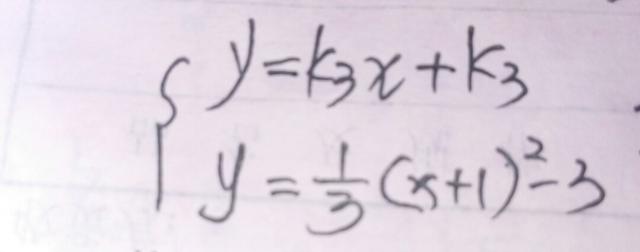
整理得，x²/3+(2/3一K3)x一(k3十8/3)=0，设该方程的两根为x1，x2，P、Q两点坐标分别为(x1，y1)，(x2，y2)，由一元二次方程根与系数关系得，x1+x2=3K3一2，则y1+y2=K3(x1+x2)十2k3=3(K3)²，由中点坐标公式得，点M坐标为(3K3/2一1，3K3²/2)，因为直线DN可由直线PQ向下平移三个单位得到，所以设直线DN的解析式为y=k3x+K3一3，它与抛物线解析式联立得，

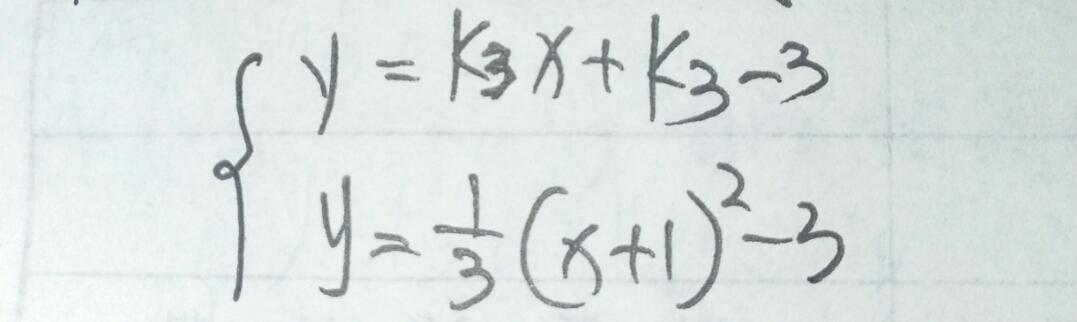
整理得，x²/3+(2/3一k3)x+1/3一k3=0，即(x+1)(x+1一3K3)=0，解得x=一1(舍去)裁x=3K3一1，代入直线DN的解析式得y=3(K3)²一3，故N点坐标为(3K3一1，3(K3)²一3)，若四边形DMPN为菱形，则DN=DM，DN²=DM²，由两点间距离公式得(3K3一1+1)²+(3K3²一3十3)²=(3K3/2一1十1)²+(3K3²/2+3)²，整理得(K3²+1)(3K3²一4)=0，解得k3=±2√3/3，因点P在第二象限，∴K3=一2√3/3，故M(一√3一1，2)，N(一2√3一1，1)，直线PQ解析式与抛物线解析式联立得，

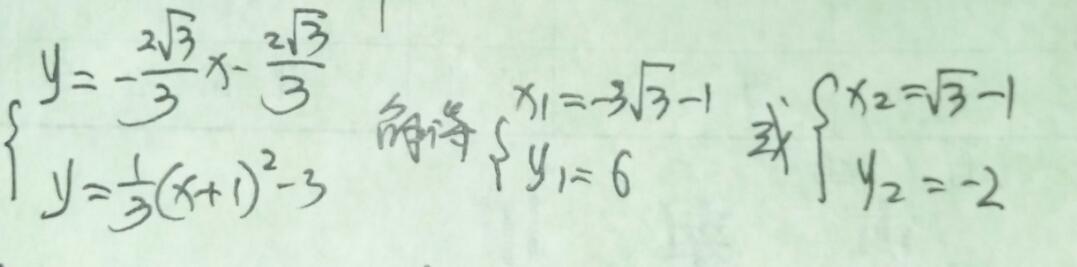
故P(一3√3一1，6)，D(一1，3)，M(一√3一1，2)，N(一2√3一1，1)，∴PM=PN=DM=DN=2√7，故四边形DM PN是菱形，此时N点坐标为(一2√3一1，1)。

【总结反思】

本题主要考查3，一次函数，二次函数的性质，分类讨论的思想，菱形的性质，对计算能力要求较高。