典型的“双垂直”模型两例

当已知条件中出现，直角(或垂直)时，我们往往通过构造垂线，形成“双直角三角形”(全等或相似)来解决问题。请看下面两例：

1.如图，以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG，连接EG，试判断△ABC与△AEG面积之间的关系，并说明理由．

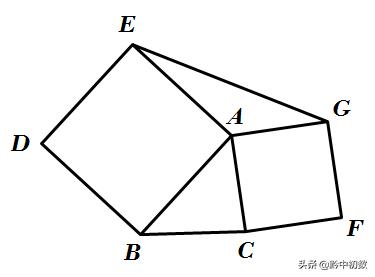
分析：△ABC与△AEG的大小必然头联系，那是什么联系呢？注意观察，两三角形有一条边相等。

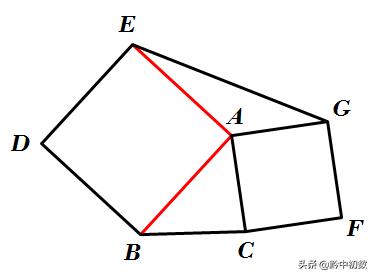
因此，既然要探索它们的面积之间的关系，所以，想到分别以这两边为底，构造它们的高。

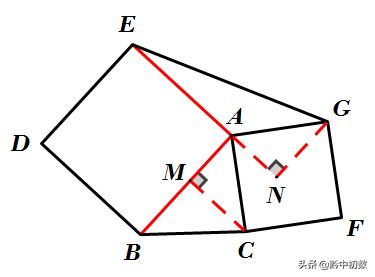
进一步思考，△AMC与△ANG正好全等。

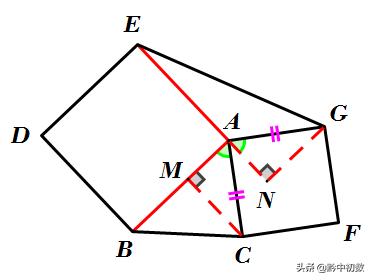
所以CM=GN,从而△ABC与△AEG的底和高分别相等。结论就显现出来了！

2.已知，如图，正方形ABCD在平面直角坐标系中，其中点A、C两点的坐标为A（6，6），C（﹣1，﹣7），则点B的坐标为______________．

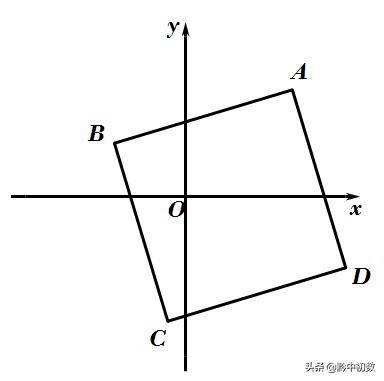
分析：作垂线，构造全等三角形，证明△ABF≌△BCG，得AF＝BG，BF＝CG，

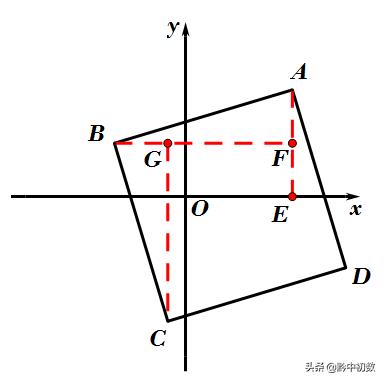
设AF＝a，FE＝b，则BF＝CG＝a+1+6＝7+b，由AE＝6＝a+b，可得a、b的值，所以根据坐标与图形特点可得结论．故答案为：（﹣4，3）．