规律探究题模型（4）——二次函数型

规律探究题模型（4）---二次函数型

规律题一般分为四种：等差型（一次函数）、循环型、等比型（相似）、二阶等差型（二次函数）。

所有的规律题目都存在一个共同的特点，就是对应，而对应恰是函数的本质特征，所以规律题目的探究本身就是函数的探究。函数有列表、图像、解析式三种表达形式，将已知条件中的对应关系列成表格形式，很容易区分属于哪种类型，最后写出对应的解析表达式

今天学习第四种类型：二阶等差型，又称为二次函数类型。

方法储备：

观察

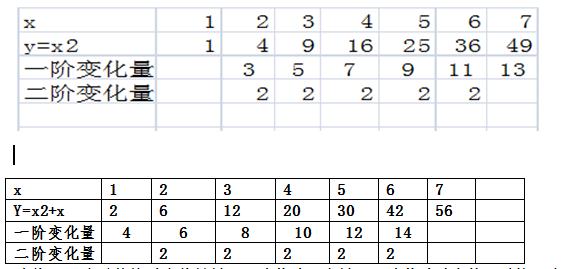
总结：二次函数的对应结果属于二阶等差，当属于二阶等差时也就可以按二次函数对待。

设y=ax2+bx+c（a≠0），代入相应的三个点的坐标即可以快速得出结果

例题：下列图形都是由同样大小的五角星按一定的规律组成，其中第①个图形一共有2个五角星，第②个图形一共有8个五角星，第③个图形一共有18个五角星，…，则第⑥个图形中五角星的个数为___.

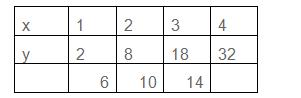
二阶变化量为相同的数值4，故为二次函数，将（1,2）、（2,8）、（3,18）代入y=ax2+bx+c（a≠0）

a+b+c=2

4a+2b+c=8

9a+3b+c=18

解方程组得出a=2 ,b=0 ,c=0 ,y=2 x2 ,第6个为2 x 6 x6 =72

特别指出：本题用此法，很多同学感觉并不简单。但是研究方法的目的是通过简单题目找出通法从而运用解决更加疑难的问题。考试中许多图形，即使认真观察，第4个、第5个的对应结果在考试中也很难找的出来（比如后面两个练习题就是这样的），把此法放在最后讲解的目的，就是通过观察，排除了等差一次函数类型、循环类型、等比相似类型，我们可以断定是二次函数类型（为什么排除前三类就能断定一定是二次函数类型，以后会给予讲解），这时候就会展示出这个方法的简洁性。

我们看一下下面这两个题目。

练习1：如图，都是由边长为1的正方体叠成的图形。例如第①个图形的表面积为6个平方单位，第②个图形的表面积为18个平方单位，第③个图形的表面积是36个平方单位。依此规律，则第⑤个图形的表面积是（ ）

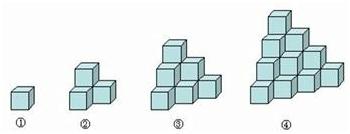
A. 90个平方单位

B. 20个平方单位

C. 89个平方单位

D. 80个平方单位

练习2：在平面直角坐标系xOy中,动点P从原点O出发,每次向上平移1个单位长度或向右平移2个单位长度,在上一次平移的基础上进行下一次平移。例如第1次平移后可能到达的点是(0,1)、(2,0),第2次平移后可能到达的点是(0,2)、(2,1)、(4,0),第3次平移后可能到达的点是(0,3)、(2,2)、(4,1)、(6,0),依此类推….我们记第1次平移后可能到达的所有点的横、纵坐标之和为l1,l1=3;第2次平移后可能到达的所有点的横、纵坐标之和为l2,l2=9;第3次平移后可能到达的所有点的横、纵坐标之和为l3,l3=18；按照这样的规律，

l4=___; ln=___(用含n的式子表示,n是正整数).

同学们仔细观察这两个题目，看一下为什么能够排除前面的三种类型，从而判断为二次函数类型的，相信你一定能够解决。