大家好,我们知道中位线也是一个很重要的知识点,在我们做题的过程中,如果能够找到中位线,或者通过做辅助线构成辅助线那么题目做起来就会变简单很多,今天就给大家分享一个中位线的专题。
首先先来说下三角形的情况,有下列情况时常作三角形中位线.
⑴有一边中点;
⑵有线段倍分关系;
⑶有两边(或两边以上)中点.
这三种情况,大家一定要记住,下面我来给大家一道例题,通过例题来熟悉。
例:如图,AE为正方形ABCD中∠BAC的平分线,AE分别交BD、BC于F、E,AC、BD相交于O,求证:OF =1/2CE
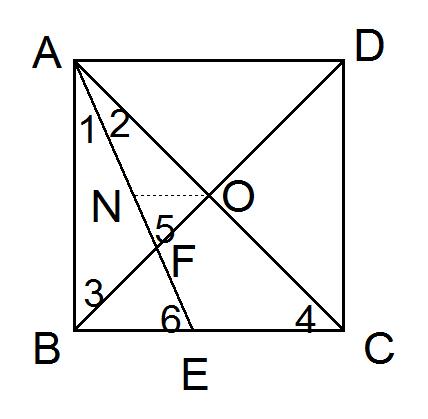
证明:取AE的中点N,连结ON,则ON为△ACE的中位线
∴ON∥CE,ON =1/2CE
∴∠6 =∠ONE
∵四边形ABCD为正方形
∴∠3 =∠4 = 45°
∴∠5 =∠3+∠1, ∠6 =∠4+∠2
∵∠1 =∠2
∴∠5 =∠6
∵∠6 =∠ONE
∴∠ONE =∠5
∴ON = OF
∴OF =1/2CE
这道题中出现正方形,我们知道正方形有个性质就是对角线互相垂直平分,那么O就是AC的中点,这就对应了上面的出现一边的中点时候可以做三角形的中位线,所以就取AE的中点做中位线,那么ON就是三角形的中位线他就等于CE的一半,我们只要证明出ON = OF,就能证出结果了,而证明ON = OF就非常简单了。
有下列情况时常构造梯形中位线
⑴有一腰中点,
⑵有两腰中点,
⑶涉及梯形上、下底和。
同样的要记住这三个条件,下面看例题:
例1:已知,如图,梯形ABCD中,AD∥BC,∠DAB = 90° ,E为CD的中点,连结AE、BE,求证:AE = BE
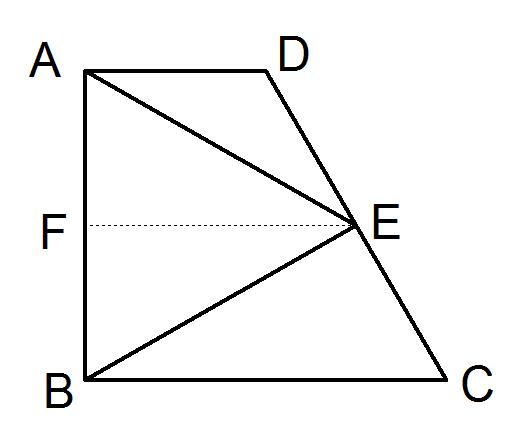
证明:取AB的中点F,连结EF,则EF∥AD
∴∠DAB =∠EFB =90°
∴EF⊥AB
∴EF为AB的中垂线
∴AE = BE
这道题做了中位线之后就变得很简单了,不再解释了,下面我们看另外一道题目:
例2:从□ABCD的顶点ABCD向形外的任意直线MN引垂线AA’、BB’、CC’、DD’,垂足分别为A’、B’、’、D’,求证:AA’+CC’ = BB’+DD’
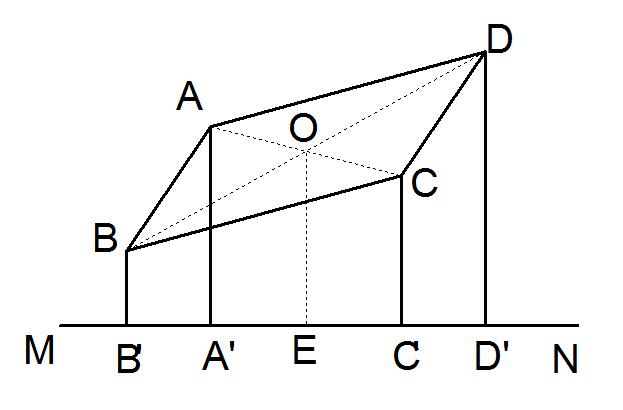
证明:连结AC、BD,它们交于点O,过O作OE⊥MN于E,则AA’∥OE∥CC’
∵四边形ABCD为平行四边形
∴AO = CO
∴A’E = C’E
∴AA’+CC’ = 2OE
同理可证:BB’+DD’ = 2OE
∴AA’+CC’ = BB’+DD’
这道题做完辅助线以后,出现了梯形CC'A'A和梯形BB'D'D两个梯形,OE都是它们的中位线,然后利用中位线的性质,通过等量替换,最后很容易得出结论。
等腰梯形的对角线与底构成的两个三角形为等腰三角形.
例:已知,如图,等腰梯形ABCD中,AB∥CD,AB>CD,AD = BC,对角线AC、BD相交于O,∠AOB = 60o ,且E、F、M分别为OD、OA、BC的中点
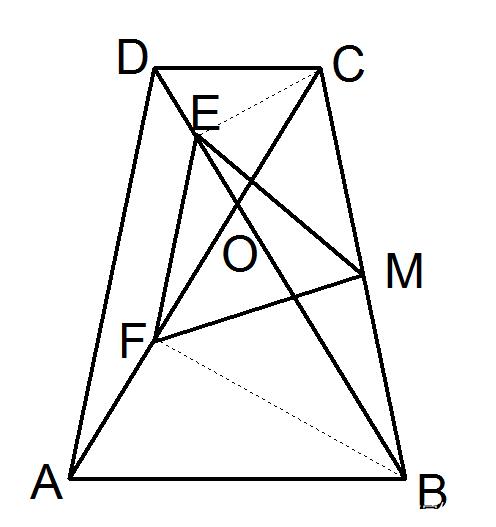
证明:连结BF、CE
∵四边形ABCD为等腰梯形
∴AD = BC,AC = BD
又∵AB为公共边
∴△ABD≌△BAC
∴∠CAB =∠DBA
∴OA = OB
∵∠AOB = 60°
∴△ABO为等边三角形
又∵F为AO中点
∴BF⊥AC
∵M为BC中点
∴MF =1/2BC
同理可证:ME =1/2BC
∵E、F分别为OD、OA中点
∴EF =1/2AD
∵AD = CB
∴ME = MF = EF
∴△MEF为等边三角形
这道题用到的知识点比较多,在例题中间证明了这个规律,这规律我们可以在填空选择题里面用,做大题的时候我们还是需要证明一下的,还用到了我们前面讲的直角三角形的性质。
连结任意四边形各边中点所得的四边形为平行四边形.
连结对角线相等的四边形中点所得的四边形为菱形.
连结对角线互相垂直的四边形各边中点所得的四边形为矩形.
连结对角线互相垂直且相等的四边形各边中点所得的四边形为正方形.
连结平行四边形、矩形、菱形、正方形、等腰梯形各边中点所得的四边形分别为平行四边形、菱形、矩形、正方形、菱形.
等腰梯形的对角线互相垂直时,梯形的高等于两底和的一半(或中位线的长)
上面这几个规律证明比较简单,大家有兴趣可以自己来,今天主要是给大家分享中位线有关的知识点,谢谢大家

 加载中,请稍侯......
加载中,请稍侯......
精彩评论