知识精要

一、概念

1. 溶质：能被溶解的纯净物质。 如，糖、盐、纯酒精等。

2. 溶剂：溶解溶质的纯净液体。 如，水、汽油等。

3. 溶液：溶质与溶剂的混合液体。 如，糖水、盐水、药水等。

4. 浓度：溶质在溶液中所占的质量百分比。

二、基本关系式

三、常见浓度题类型

典型例题

例1 在含糖量为 7％ 的 600 克糖水中，加入多少克水就能得到浓度为 3％ 的糖水？

算术法：

含糖：600×7％ = 42（克）

3％糖水共： 42÷ 3％ = 1400（克）

加入水量：1400 – 600= 800（克）

答：加入 800 克水就能得到浓度为 3％ 的糖水。

方程法：

解：设加入x克水后得到 3％ 的糖水。由题意得：

3%（600+x）=600×7% 解之，得x=800

答：加入 800 克水就能得到浓度为 3％ 的糖水。

例2 一容器内有浓度为 25％的糖水，若再加入 20 千克水，则糖水的浓度变为 15％，问这个容器内原来含有糖多少千克？

解：设 25％的糖水原有x千克， 由题意得：

25%x=15%(x+20) 解之,得x=30

原来含糖：25%x=7.5(千克)

答：这个容器内原来含有糖 7.5 千克。

例3 甲、乙两只装满硫酸溶液的容器，甲容器中装有浓度为 8％的硫酸溶液 600 千克，乙容器中装有浓度为 40％的硫酸溶液 400 千克。问从甲、乙两容器中各取多少相同千克数的溶液分别放入对方容器中，才能使这两个容器中的硫酸溶液的浓度一样？

算术法：

混后浓度都是：（600×8％+ 400×40％）÷（600 + 400）= 20.8％

混后甲增纯酸：600×20.8％– 600×8％ = 76.8（kg）

各取互换质量： 76.8÷（40％– 8％）= 240（kg）

答：应从两容器中各取 240 千克溶液分别放入对方容器中，才能使这两个容器中的硫酸溶液的浓度一样。

方程法：

解：设从甲、乙各取x千克硫酸互换放入后，能使甲、乙中硫酸浓度相等。这时

甲中纯酸：8%(600-x)+40%x=48+32%x

乙中纯酸：40%(400-x)+8%x=160-32%x

(48+32%x)÷600=(160-32%x)÷400 解之,得x=240

答：应从两容器中各取 240 千克溶液分别放入对方容器中，才能使这两个容器中的硫酸溶液的浓度一样。

此题公式是：600×400÷（600+400）=240（千克）

总结此类题公式如下：

例4 现有浓度为 10％的糖水 20 千克，问再加入多少千克浓度为 30％的糖水，可以得到浓度为 22％ 的糖水？

算术法：

混后 20 kg中多纯糖： 20×22％– 20×10％=2.4（kg）

加入 30％ 糖水质量： 2.4÷ （30％– 22%） = 30（kg）

答：需再加入 30 千克浓度为 30％ 的糖水，才能得到浓度为 22％ 的糖水。

方程法：

解：设需再加入x千克30％的糖水后，就可得到22％的糖水。由题意得

20×10%+30%x=(x+20)×22% 解之，得x=30

答：需再加入 30 千克浓度为 30％ 的糖水，才能得到浓度为 22％ 的糖水。

例5 把浓度为 20％、30％和 45％的三种酒精溶液混合在一起，得到浓度为 35％的酒精溶液 45 升。已知浓度为 20％的酒精溶液用量是浓度为 30％的酒精溶液用量的 3 倍。问原来每种浓度的酒精溶液各用了多少升？

解：设 30％的酒精用x升， 则 20％的酒精用 3x升,则 45％的酒精用45-x-3x=45-4x升.由题意得。

（等量关系： 混前纯酒精和 = 混后纯酒精）

30%x+20%×3x+45%×（45-4x）=45×35% 解之，得x=5

20%的用：5×3=15（升）

45%的用：45-5×4=25（升）

答：浓度为 20％、30％和 45％的酒精溶液分别用了 15 升、5 升和 25 升。

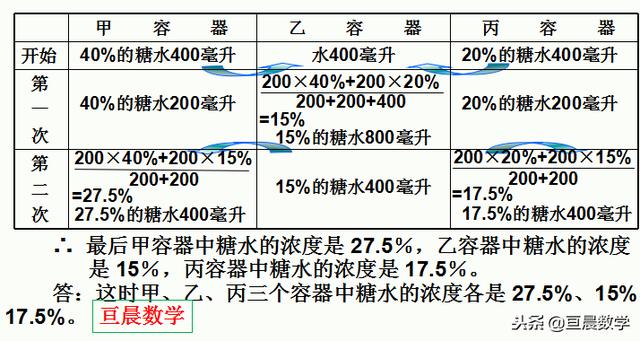
例6 有甲、乙、丙三个容量为 1000 毫升的容器。甲容器有浓度为 40% 的糖水 400 毫升，乙容器中有清水 400 毫升，丙容器中有浓度为 20% 的糖水 400 毫升。先把甲、丙两容器中的糖水各一半倒入乙容器搅匀后，再把乙容器中的糖水 200 毫升倒入甲容器， 200 毫升倒入丙容器。问这时甲、乙、丙三个容器中糖水的浓度各是多少？

解析如下：

列表求解，直观明了