三角形有关的二次函数动点问题

与三角形有关的二次函数动点问题，讲解分析1：

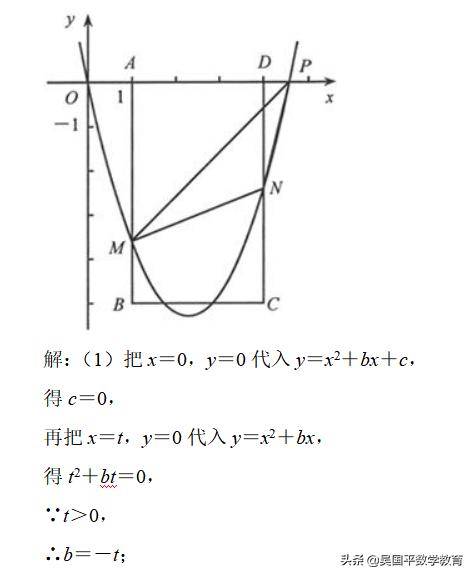
如图，在平面直角坐标系中，点P从原点O出发，沿x轴向右以毎秒1个单位长的速度运动t秒（t＞0），抛物线y＝x2＋bx＋c经过点O和点P，已知矩形ABCD的三个顶点

为 A （1，0），B （1，－5），D （4，0）．

（1）求c，b （用含t的代数式表示）：

（2）当4＜t＜5时，设抛物线分别与线段AB，CD交于点M，N．

①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；

②求△MPN的面积S与t的函数关系式，并求t为何值时，S=21/8；

（3）在矩形ABCD的内部（不含边界），把横．纵 坐标都是整数的点称为“好点”．若抛物线将这些“好点”分成数量相等的两部分，请直接写出t的取值范围．

考点分析：

二次函数综合题。

题干分析：

（1）由抛物线y＝x2＋bx＋c经过点O和点P，将点O与P的坐标代入方程即可求得c，b；

（2）①当x＝1时，y＝1－t，求得M的坐标，则可求得∠AMP的度数，

②由S＝S四边形AMNP－S△PAM＝S△DPN＋S梯形NDAM－S△PAM，即可求得关于t的二次函数，列方程即可求得t的值；

（3）根据图形，即可直接求得答案．

解题反思：

此题考查了二次函数与点的关系，以及三角形面积的求解方法等知识．此题综合性很强，难度适中，解题的关键是注意数形结合与方程思想的应用．

与三角形有关的二次函数动点问题，讲解分析2：

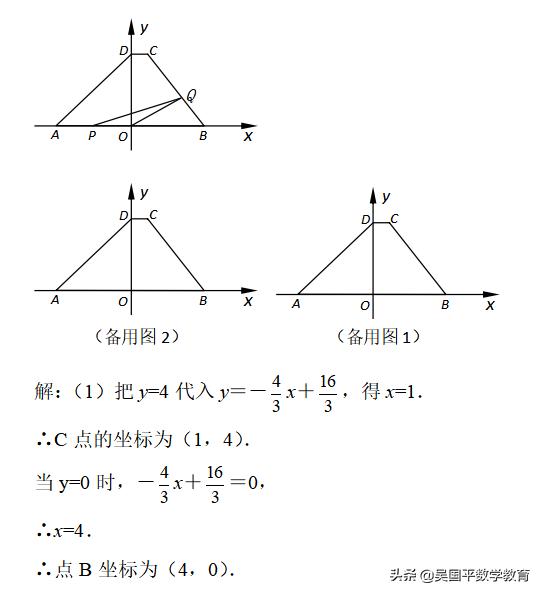
如图，在直角坐标系中，梯形ABCD的底边AB在x轴上，底边CD的端点D在y轴上.直线CB的表达式为y=－4x/3+16/3，点A、D的坐标分别为（－4，0），（0，4）.动点P自A点出发，在AB上匀速运行.动点Q自点B出发，在折线BCD上匀速运行，速度均为每秒1个单位.当其中一个动点到达终点时，它们同时停止运动.设点P运动t（秒）时，△OPQ的面积为s（不能构成△OPQ的动点除外）.

（1）求出点B、C的坐标；

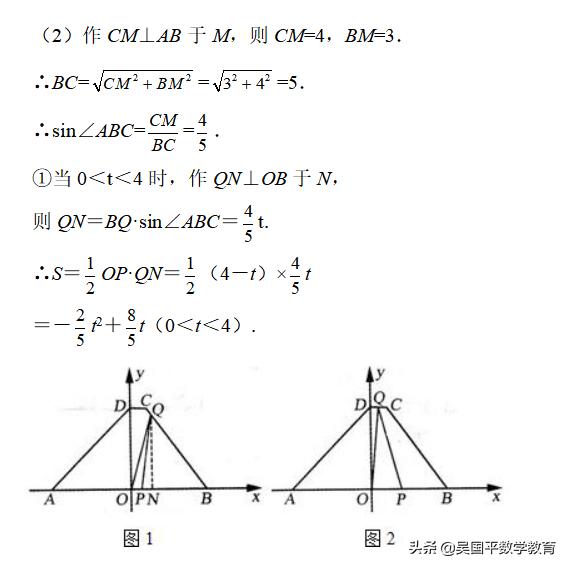
（2）求s随t变化的函数关系式；

（3）当t为何值时s有最大值？并求出最大值.

考点分析：

二次函数综合题.

题干分析：

（1）把y=4代入y=－4x/3+16/3求得x的值，则可得点C的坐标，把y=0代入y=－4x/3+16/3求得x的值，即可得点B的坐标；

（2）作CM⊥AB于M，则可求得CM与BM的值，求得∠ABC的正弦值，然后分别从0＜t＜4时，当4＜t≤5时与当5＜t≤6时去分析求解即可求得答案；

（3）在（2）的情况下s的最大值，然后比较即可求得答案．

解题反思：

此题考查了点与函数的关系，三角形面积的求解方法以及利用二次函数的知识求函数的最大值的问题．此题综合性很强，难度较大，解题时要注意分类讨论思想，方程思想与数形结合思想的应用．

近年来，最值问题频繁出现在中考数学压轴题中，而最值问题一直是数学的重难点，它要求学生具有很强的问题分析能力与综合运用数学知识、数学思想方法解决问题的能力。

抛物线中动点三角形面积最大值问题是初中二次函数这一知识板块的重点和难点，更是初中高中数学知识的衔接点，因此大家一定要认真对待。

与三角形有关的二次函数动点问题，讲解分析3：

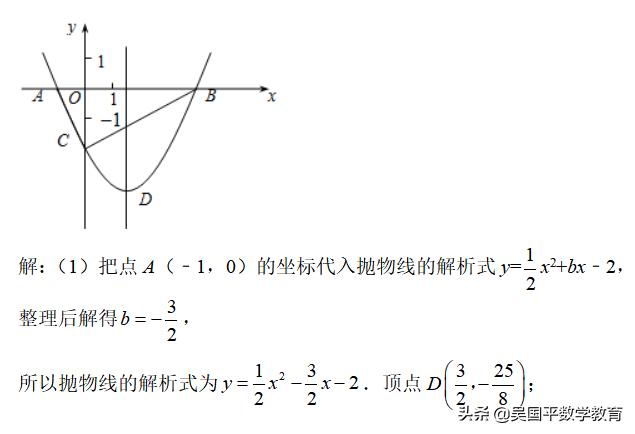
如图，抛物线y=x2/2+bx﹣2与x轴交于A，B两点，与y轴交于C点，且A（﹣1，0）．

（1）求抛物线的解析式及顶点D的坐标；

（2）判断△ABC的形状，证明你的结论；

（3）点M（m，0）是x轴上的一个动点，当MC+MD的值最小时，求m的值．

考点分析：

二次函数综合题．

题干分析：

（1）把A点的坐标代入抛物线解析式，求b得值，即可的出抛物线的解析式，根据顶点坐标公式，即可求出顶点坐标；

（2）根据直角三角形的性质，推出AC2=OA2+OC2=5，BC2=OC2+OB2=20，即AC2+BC2=25=AB2，即可确△ABC是直角三角形；

（3）作出点C关于x轴的对称点C′，则C′（0，2），OC'=2．连接C'D交x轴于点M，根据轴对称性及两点之间线段最短可知，MC+MD的值最小．首先确定最小值，然后根据三角形相似的有关性质定理，求m的值

解题反思：

本题着重考查了待定系数法求二次函数解析式．直角三角形的性质及判定．轴对称性质以及相似三角形的性质，关键在于求出函数表达式，做好辅助点，找对相似三角形．

中考数学压轴题考查学生综合知识的运用能力，此类题由于集平面几何、函数及方程等相关知识于一身，题型的灵活性强难度大，让许多考生都倍感压力。要想拿到此块知识内容的分数，不仅要学好知识定理，更要不断提升分析问题和解决问题的能力。