九下：学霸易错题，一次、反比函数与直线存在交点，求K的范围

1如图,Rt△ABC位于第一象限内,A点的坐标为(1,1),两条直角边AB、AC分别平行于x轴、y轴,AB=4,AC=3,若正比例函数函数y=kx的图象与Rt△ABC有交点，则k的取值范围是（ ）

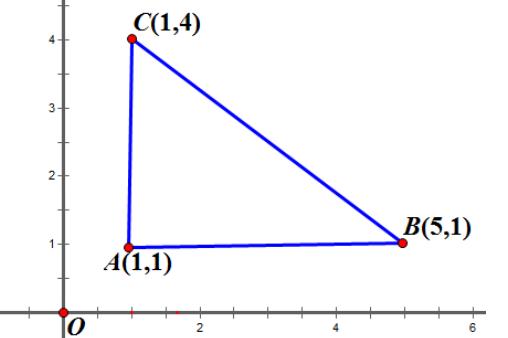
分析：正比例函数是直线型，代入三点坐标，找出最大、最小值，即可得出K的取值范围

2如图,Rt△ABC位于第一象限内,A点的坐标为(1,1),两条直角边AB、AC分别平行于x轴、y轴,AB=4,AC=3,若反比例函数y=k/x(k>0)的图象与Rt△ABC有交点，则k的取值范围（ ）

分析：图形不变，其他条件不变，仅仅正比例函数改为了反比例函数，些微差别，难度大大增加，先看下图

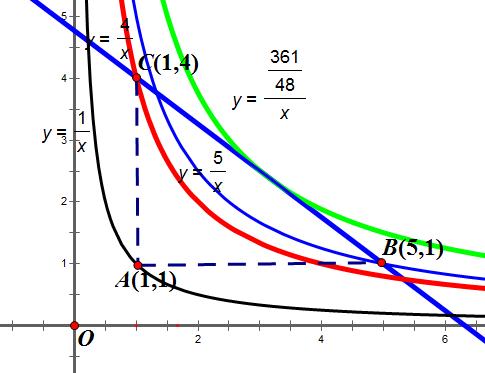
显然，过A 、B、C三点的反比例函数都是与直线BC有两个交点，代入A得到K的最小值为1，而代入B 、C得到的K值分别为5 ，4 ；而5并不是K的最大值，最大值应该是反比例函数y=k/x与直线BC相切，也就是仅一个公共点时的K值。

解决方法：求交点必列方程组，

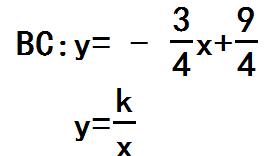
转化为一元二次方程，当判别式为0时，二者仅有一个交点，即此时相切，得到K=361/48,即为最大值

练习：

3如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数y=k/x

在第一象限内的图象与△ABC有交点，则k的取值范围是___.

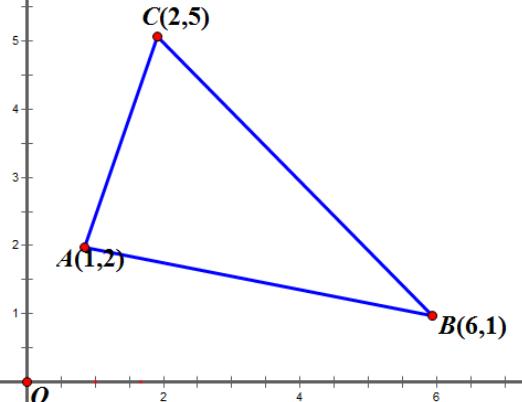
看图说话

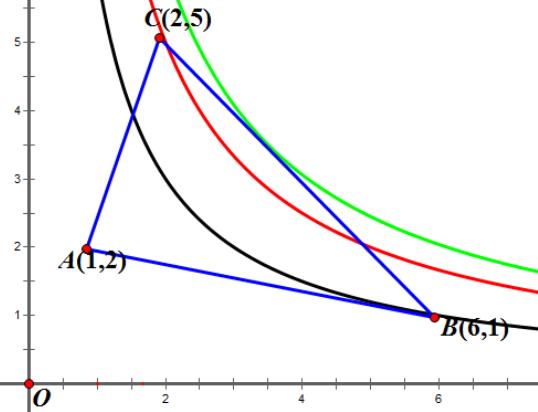
试一试，自我完成。注意总结直线型与曲线型函数交点的区别。