一题贯穿二次函数综合（二）——角的存在性问题

二次函数中角的存在性问题，大致可分为两大类：（1）角的顶点坐标已知；（2）角的顶点坐标未知.本专题我们就沿着这两种情况展开探究.

如图，抛物线y=-x^2+2x+3与x轴交于A，B两点(点A在点B的左侧)，与y轴交于点C.

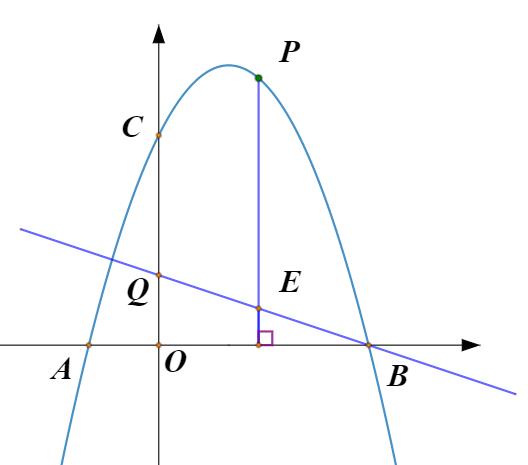
（6）已知点Q（0,1），P是抛物线上一个动点，过点P作x轴的垂线，交BQ于点E，是否存在点P使得∠PBE=45°.若存在求出点P的坐标；若不存在，请说明理由.

解法一分析：由∠PBE=45°，所以过点P作PM⊥BQ，则△PBM是等腰直角三角形。依托直角∠PMB构造K形图（关于K形图可参阅K形图在河南中考压轴题中的运用），先设出点M的坐标，进而表示出点P的坐标，再把点P的坐标代入抛物线解析式，解方程即可。

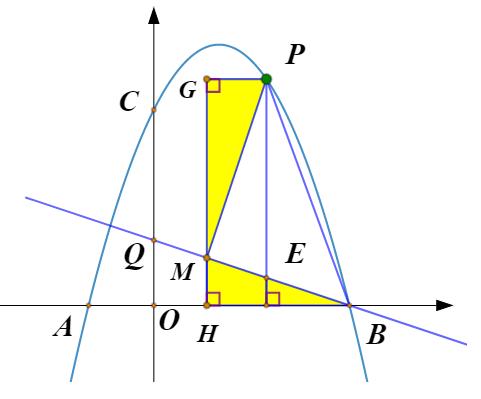
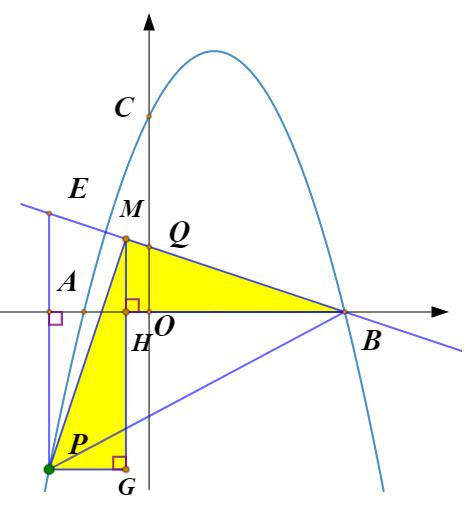
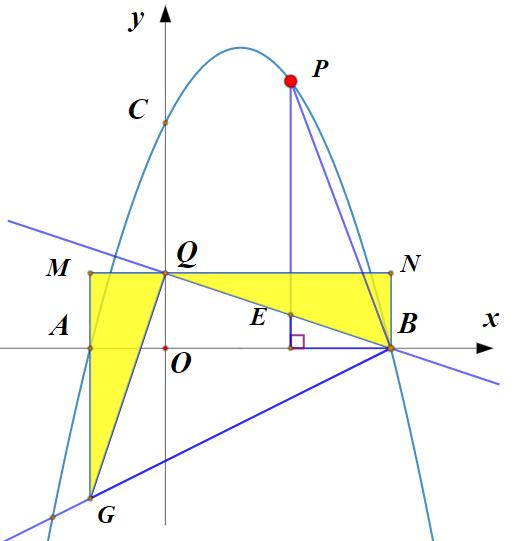
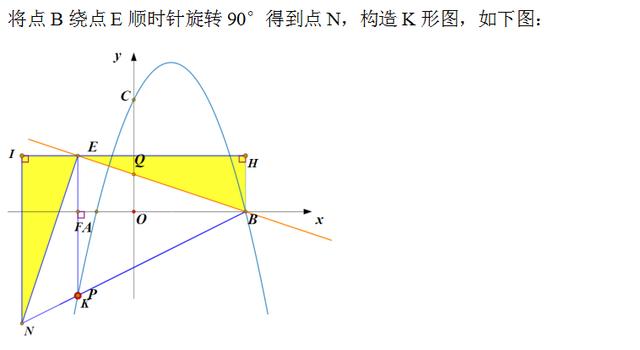
解法二分析：读题可知，点E始终在BQ上运动，所以∠PBE=∠PBQ=45°，见到45°，我们会联想到等腰直角三角形，将点B绕着点Q旋转90°得到点G，则∠GBE=45°，延长BG和抛物线相交，交点即为所求的点P.

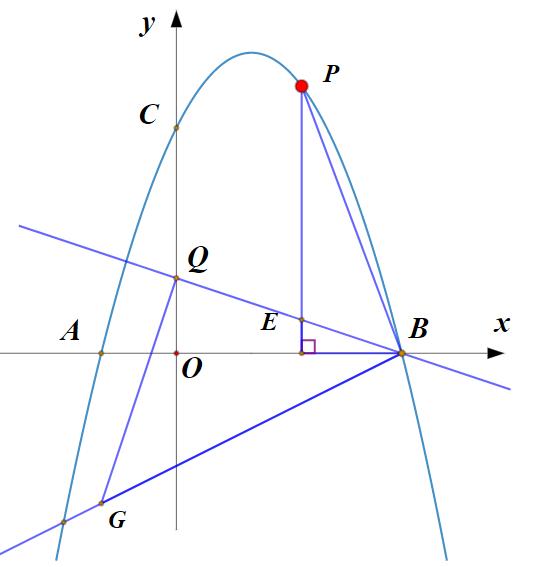
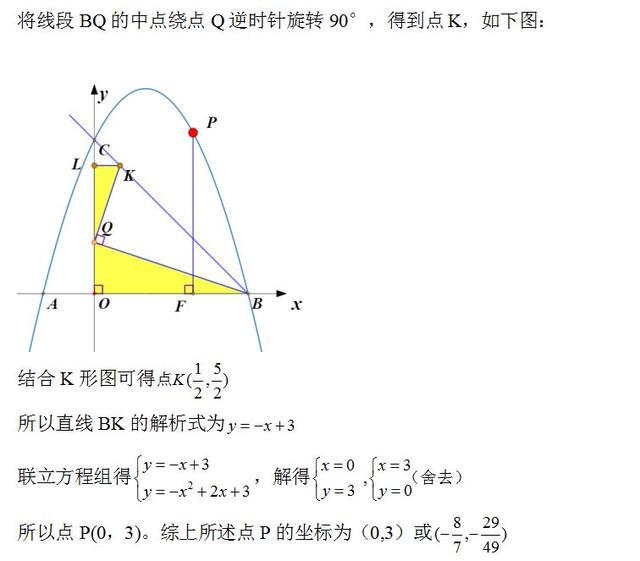
关于点P的坐标的求法，可先构造K形图（如下图），求出点G的坐标。由于点B、点G的坐标已知，可求出直线BG的解析式，将直线BG解析式和抛物线的解析式联立方程组即可求得点P的坐标.

用同样的方法可求出另一满足要求的点P。将点B绕点Q逆时针旋转90°，得到图中的点H，直线BH与抛物线的交点即为所求的点P，本题中点H刚好就是点P。

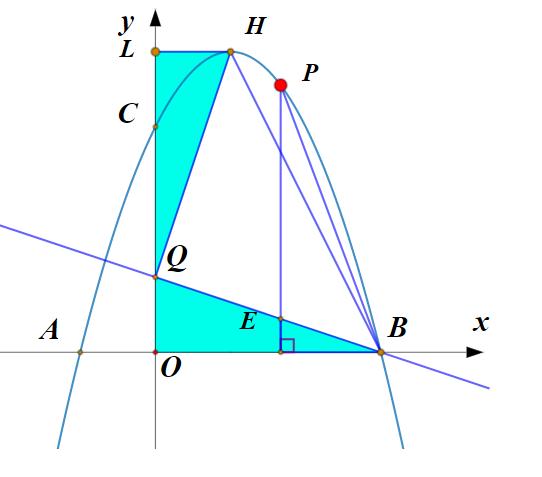
解法三分析：解法二中是通过将点B绕着点Q旋转90°，构造等腰直角三角形。当然我们也可以将点B绕点E旋转90°，构造等腰直角三角形.

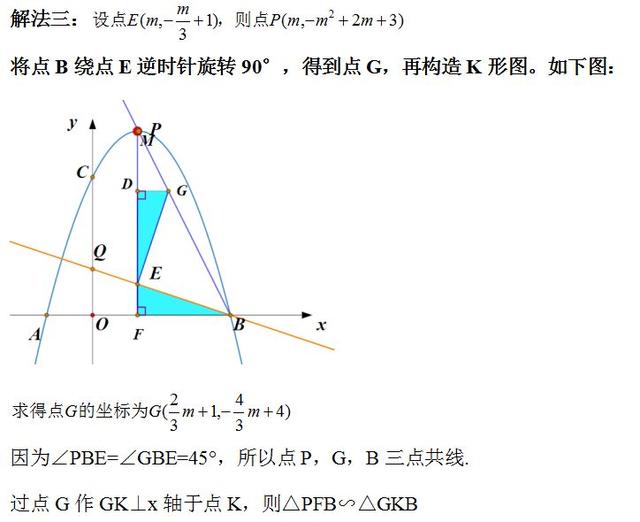
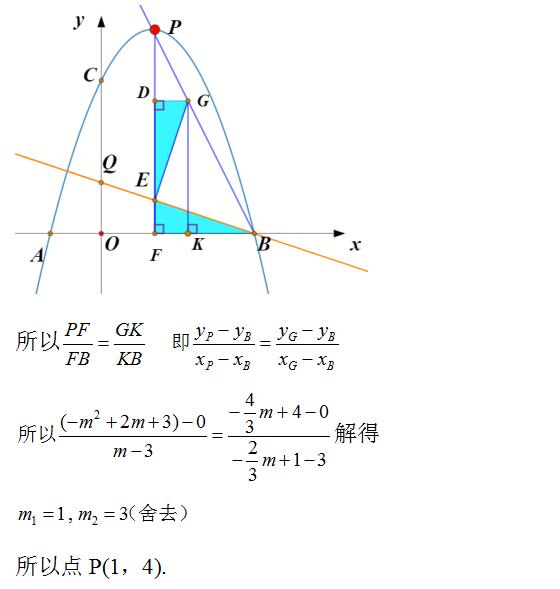
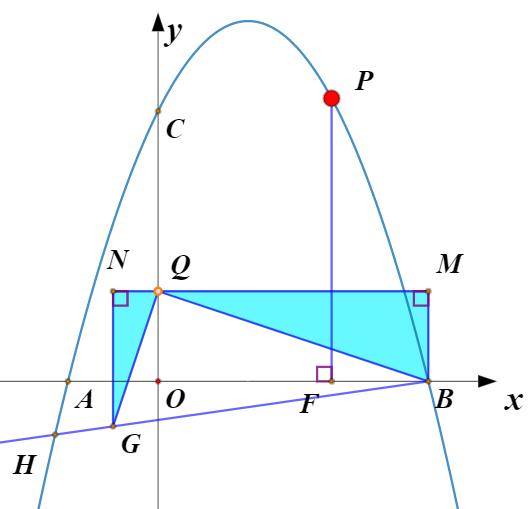
（7）已知点Q（0,1），P是抛物线上一个动点，过点P作x轴的垂线，交BQ于点E，是否存在点P使得tan∠PBE=1/2.若存在求出点P的坐标；若不存在，请说明理由.