初中数学一元二次方程知识点总结（含方法技巧归纳，易错辨析）

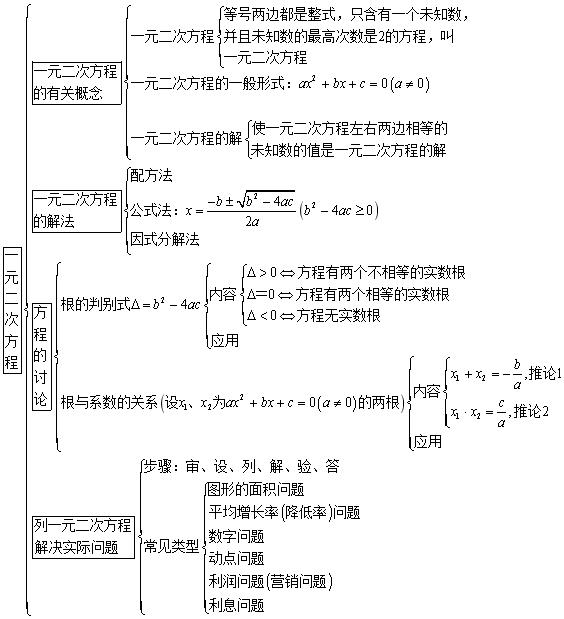
1一元二次方程的定义及一般形式

定义：等号两边都是整式，只含有一个未知数(一元)，并且未知数的最高次数是2(二次)的方程，叫作一元二次方程.

点拨

对定义的理解抓住三个条件：“一元”“二次”“整式方程”,缺一不可，同时强调二次项的系数不为0.

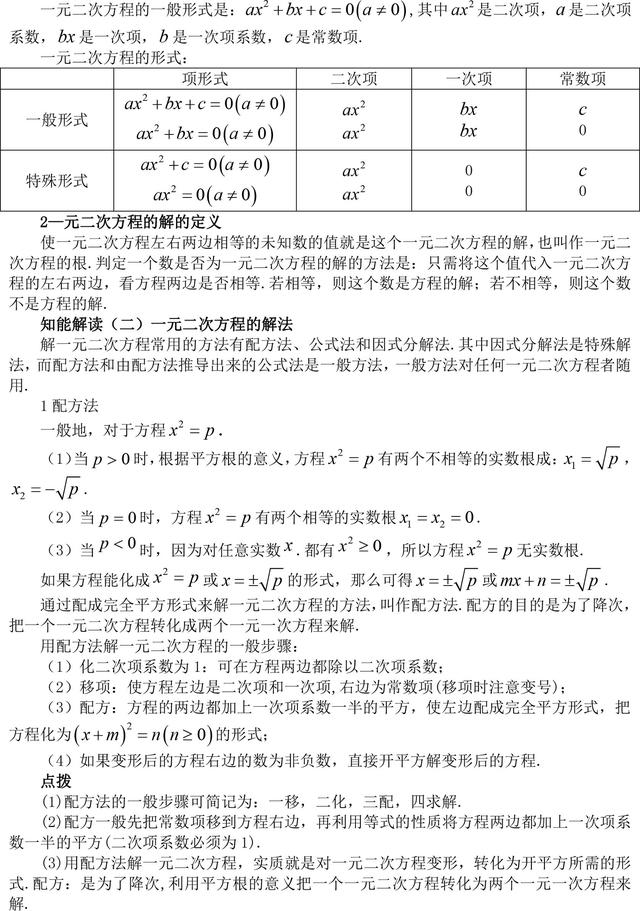
用公式法解一元二次方程的记忆口诀

要用公式解方程，首先化成一般式.

调整系数随其后，使其成为最简比.

确定参数

，计算方程判别式.

判别式值与零比，有无实根便得知.

若有实根套公式，若无实根要告之.

3因式分解法

通过因式分解，使一元二次方程化为两个一次式的乘积等于0的形式，再使这两个一次式分别等于0,从而实现降次，这种解一元二次方程的方法叫作因式分懈法.

因式分解法体现了将一元二次方程“降次”转化为一元一次方程来解的思想，运用这种方法的步骤：

（1）将所有项移到方程的左边，将方程的右边化为0；

（2）将方程左边分解为两个一次因式的乘积；

（3）令每个因式分别等于零，得到两个一元一次方程；

（4）解这两个一元一次方程，他们的解就是原方程的解.